Test T studenta w praktyce

Celem niniejszego artykułu jest przedstawienie praktycznego wykorzystania jednego z najpopularniejszych testów (test T) statystycznych wykorzystywanych w przemyśle.
Test t Studenta jest często stosowanym w praktyce parametrycznym testem istotności. Za jego pomocą weryfikacji poddaje się różnice wartości średnich z pomiarów w dwóch próbach.
Test T – główne założenia:
- Badane są dwie próby z populacji mających rozkłady normalne.
- Parametry tych rozkładów nie są znane, ale spełniony jest warunek σ1 = σ2 (występuje jednorodność wariancji w populacjach).
Podczas testowania weryfikacji poddaje się hipotezę zerową:
H0: m1=m2 (średnie z dwóch prób są równe)
wobec hipotezy alternatywnej przedstawionej w trzech wariantach:
1. H1: m1 ≠ m2 – weryfikacja dwustronnego obszaru krytycznego
2. H1: m1 < m2 – weryfikacja lewostronnego obszaru krytycznego
3. H1: m1 > m2 – weryfikacja prawostronnego obszaru krytycznego
Test T – przebieg:
- Estymacja wartości średnich arytmetycznych, wariancji oraz liczebności prób n1, n2.
- Obliczenie statystyki t Studenta wg wzoru:
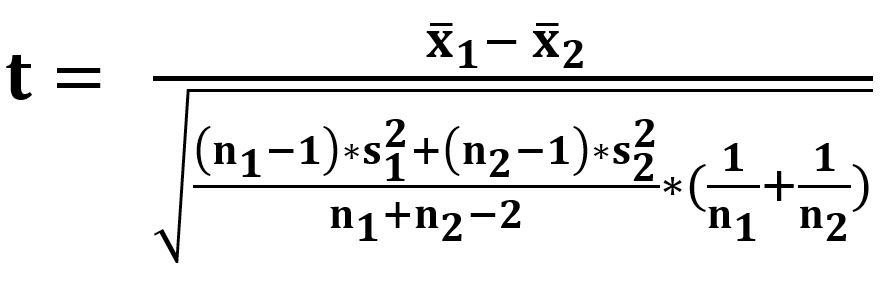
która przy założeniu prawdziwości H0 ma rozkład t Studenta o liczbie swobody równej n1 +n2-2.
Test T – praktyczny przykład zastosowania:
W przedsiębiorstwie produkującym w systemie dwuzmianowym (zmiana A i zmiana B) inżynier jakości postanowił wykonać analizę zdolności oraz wydajności procesu kontroli śruby mocującej jeden z kluczowych elementów wyrobu.
W tym celu zapisy pomiarów z dwóch zmian z ostatniego miesiąca (niestety gromadzone tylko w wersji papierowej) wprowadził do arkusza programu Minitab w wersji 19. Wynik analizy przedstawiono na Rys.1.

W wyniku analizy inżynier stwierdził, że ponieważ wartości wskaźników Cp/Cpk oraz Pp/Ppk są niskie (niższe niż przyjęta wartość krytyczna 1,33) proces kontroli momentu dokręcenia na śrubie należy doskonalić.
Stwierdzenie słuszne…
….ale inżynier pominął jeden ważny krok analizy. Ponieważ dane pochodzą z dwóch różnych źródeł (strumieni): zmiana A i zmiana B, przed wykonaniem analizy zdolności i wydajności procesu należy wykonać testy na jednorodność wariancji oraz na jednorodność wartości średnich arytmetycznych w próbach.
O tym, iż być może wartości średnie nie są takie same, świadczyć może kształt histogramu na Rys. 1 – widoczny zarys dwu-modalności histogramu.
W związku z tym za namową konsultanta wykonano dodatkowe testy statystyczne:
- Na zgodność danych z rozkładem normalnym – wynik OK (H0 nie została odrzucona na poziomie α0,05).
- Test F dla jednorodności wariancji – wynik OK (H0 nie została odrzucona na poziomie α0,05).
- Test T Studenta dla porównania wartości średnich w próbach – wynik NOK (H0 została odrzucona na poziomie α0,05). Wynik testu przedstawiono na Rys. 2 i Rys.3.


W wyniku testu t Studenta stwierdzono, że wartości średnie pomiarów z dwóch zmian nie są takie same i różnią się od siebie średnio o 20,8 Nm. Oznacza to, iż należy dokonać analizy, dlaczego pomiarowcy z różnych zmian wykonują pomiary różnie (brak odtwarzalności pomiarowej).
Dodatkowo z wykresu punktowego – Rys.3 – wynika, że to kontroler ze zmiany A powoduje obniżenie wskaźników zdolności i wydajności procesu i to pomiarom tego kontrolera należy się przyjrzeć w pierwszej kolejności.
W sytuacji, kiedy istnieje statystyczna różnica pomiędzy wartościami średniej arytmetycznej w próbach, estymacji wskaźników procesu należy dokonać oddzielnie dla każdej zmiany. Analizę taką przedstawiono na Rys. 4.

Podsumowanie
W artykule przedstawiono zastosowanie parametrycznego testu t Studenta dla dwóch średnich przy założeniu jednorodności wariancji. Test ten jest podstawowym narzędziem wykorzystywanym w wielu sytuacjach produkcyjnych tj. rozwiązywanie problemów, regulacja procesów czy tak jak przedstawiono w artykule przed wykonaniem analizy zdolności i wydajności procesu. Pominięcie tego testu może dostarczyć niekompletnych informacji co wiązać się może ze wzrostem kosztów produkcji. Test t Studenta jest również dostępny dla sytuacji, w której zmienność w próbach nie jest taka sama (niejednorodność wariancji).
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
