Testy t-Studenta z dodatkiem MS Excel Analysis ToolPak

Testy t-Studenta – wstęp
W niniejszym artykule przedstawiono wykorzystanie trzech popularnych i często używanych w praktyce parametrycznych testów istotności. Testy t-Studenta służą do badania dwóch prób z podziałem na próby zależne i niezależne.
Testy t stosuje się w sytuacji, w której badane populacje mają rozkłady normalne, a parametry tych rozkładów nie są znane.
Tu należy zaznaczyć, że rozkład normalny stanowi odpowiedni kontekst do interpretacji wartości standaryzowanych, lecz nie jest odpowiednim punktem odniesienia dla statystyki t. Rozkład t-Studenta wygląda bardzo podobnie do rozkładu normalnego, jednak nie identycznie.
Szczególnie przy testowaniu prób o niewielkiej liczności ich zastosowanie może przynieść istotne różnice w wynikach zawierających prawdopodobieństwo. Na Rys. 1 przedstawiono rozkład t-Studenta w sąsiedztwie krzywej normalnej.
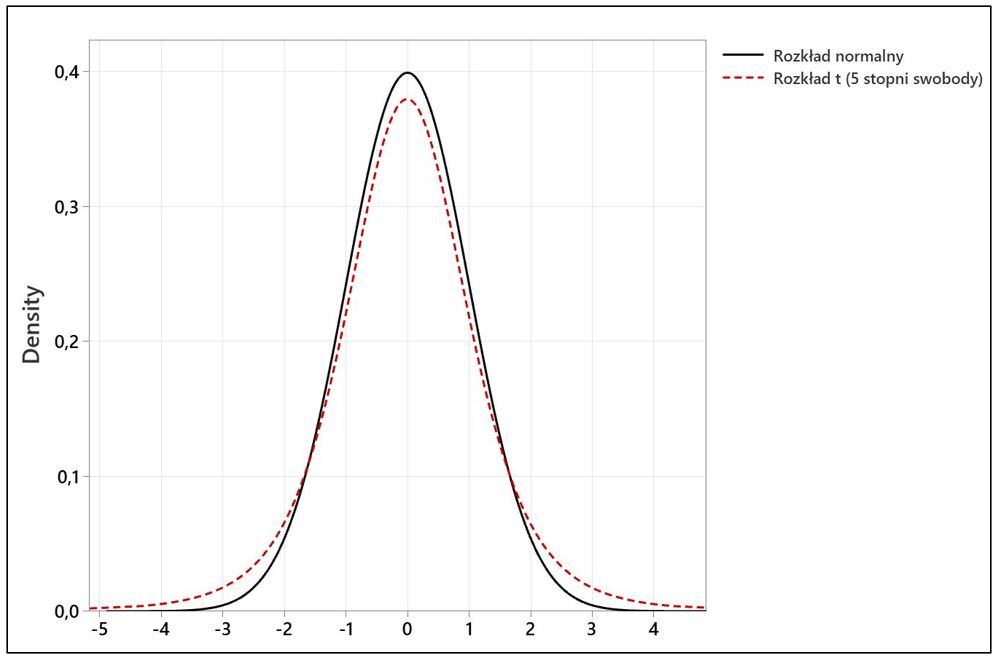
Zauważyć można, że rozkład t-Studenta jest niższy w punkcie maksimum (mniejsze prawdopodobieństwo obserwacji w pobliżu średniej) i grubszy w ogonach rozkładu (wyższe prawdopodobieństwo obserwacji).
Rozkład t-Studenta przedstawiony na Rys. 1 jest rozkładem z 5 stopniami swobody. Gdy liczba stopni swobody rośnie, kształt rozkładu t staje się coraz bardziej zbliżony do rozkładu normalnego.
TEORIA
Testy t-Studenta dla dwóch średnich (równe wariancje) – próby niezależne
Test ten jest jednym z najczęściej stosowanym w praktyce parametrycznym testem istotności. Za jego pomocą weryfikacji poddaje się różnicę wartości średnich z pomiarów (obserwacji).
Założenia testu:
- Badane są dwie próby z populacji mających rozkłady normalne N(m1, σ1) i N(m2, σ2).
- Parametry tych rozkładów nie są znane, ale spełniony jest warunek σ1 = σ2 (równość wariancji).
- Próby są niezależne.
Weryfikacji poddaje się hipotezę zerową:
H0: m1=m2
wobec hipotezy alternatywnej w trzech wariantach:
H1: m1 ≠ m2 – weryfikacja dwustronnego obszaru krytycznego
H1: m1 < m2 – weryfikacja lewostronnego obszaru krytycznego
H1: m1 > m2 – weryfikacja prawostronnego obszaru krytycznego
Wyniki obydwu prób wykorzystuje się do obliczenia estymatorów wartości średnich arytmetycznych, nieobciążonych estymatorów wariancji, a następnie uwzględniając liczebności prób, wartość statystyki:
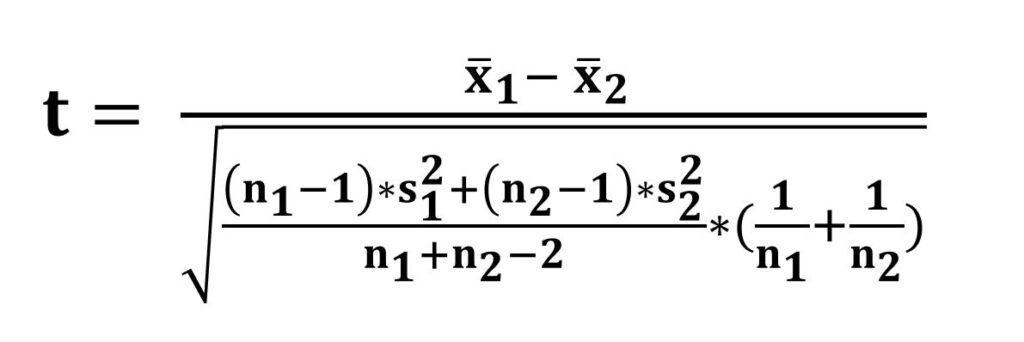
Statystyka ta, przy założeniu prawdziwości H0, ma rozkład t-Studenta o liczbie stopni swobody równej (n1+n2)-2.
Przed wykonaniem tego testu należy potwierdzić normalność rozkładu (np. test Shapiro-Wilka) oraz jednorodność wariancji (np. test F).
Testy t-Studenta dla dwóch średnich (nierówne wariancje)- próby niezależne
Jeżeli wynik testu F wskazuje na odrzucenie hipotezy zerowej (wariancje w próbach są nierówne) do porównania wartości średnich wykorzystywany jest test t-Studenta dla nierównych wariancji z poprawką Satterwhite’a. Test ten polega na obliczeniu wartości statystyki:

Statystyka ta, przy założeniu prawdziwości H0, ma rozkład t-Studenta o liczbie stopni swobody równej:
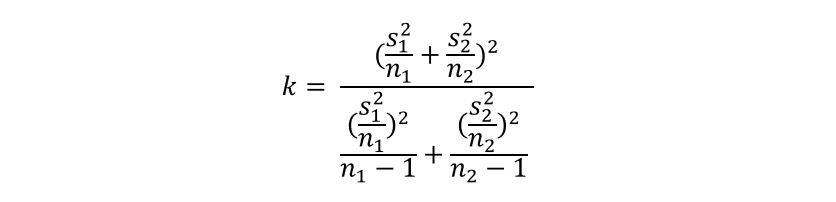
Przed wykonaniem tego testu należy wykonać badanie normalności rozkładów prób.
Testy t-Studenta dla par skojarzonych – próby zależne
Test ten służy do dwukrotnej weryfikacji danych jednej populacji, w pewnym odstępie czasu, w którym dane zostały poddane wpływowi jakiegoś czynnika zewnętrznego. Próba składa się z n elementów, z których każdy był poddany dwukrotnym pomiarom (każdy z tych obiektów charakteryzuje para liczb).
Innym wykorzystaniem testu t-Studenta dla par skojarzonych jest dwukrotny pomiar tej samej cechy, ale za pomocą dwóch różnych metod (narzędzi) pomiarowych.
W teście tym weryfikowana jest średnia różnica dwóch serii pomiarowych a nie różnica ich wartości średnich.
Przebieg testu:
Dla każdej pary skojarzonej oblicza się różnicę pomiarów (zalecany sposób: „po” minus „przed”). Jeżeli wynik pomiaru „przed” oznaczamy Xi a pomiaru „po” Yi to różnica Zi =Yi – Xi będzie dodatnia, gdy zaobserwujemy wzrost badanej cechy i ujemna gdy spadek.
Weryfikacji poddaje się hipotezę zerową:
H0: Zśr = 0 – brak wpływu zastosowanej operacji bądź zmiany metody
wobec hipotezy alternatywnej (H1) w trzech wariantach:
Zśr ≠ 0 – istotna zmiana (dwustronny obszar krytyczny)
Zśr > 0 – istotny wzrost (prawostronny obszar krytyczny)
Zśr < 0 – istotny spadek (lewostronny obszar krytyczny)
Na postawie różnic wyników pomiarów oblicza się średnią różnicę oraz estymator odchylenia standardowego różnic, a następnie wartość statystyki:
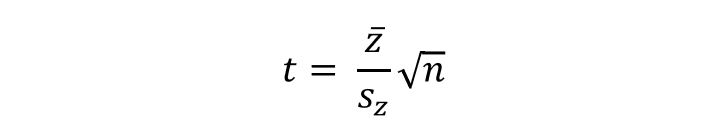
Statystka ta, przy założeniu prawdziwości H0 ma rozkład t-Studenta o n-1 stopniach swobody.
Testy t-Studenta z dodatkiem MS Excel Analysis ToolPak
Wszystkie trzy testy wykonać można z pomocą zautomatyzowanej opcji programu MS Excel: Analysis ToolPak.
W zakładce Dane należy kliknąć na Analiza Danych, po którym uruchomione zostanie okno jak na Rys. 2.
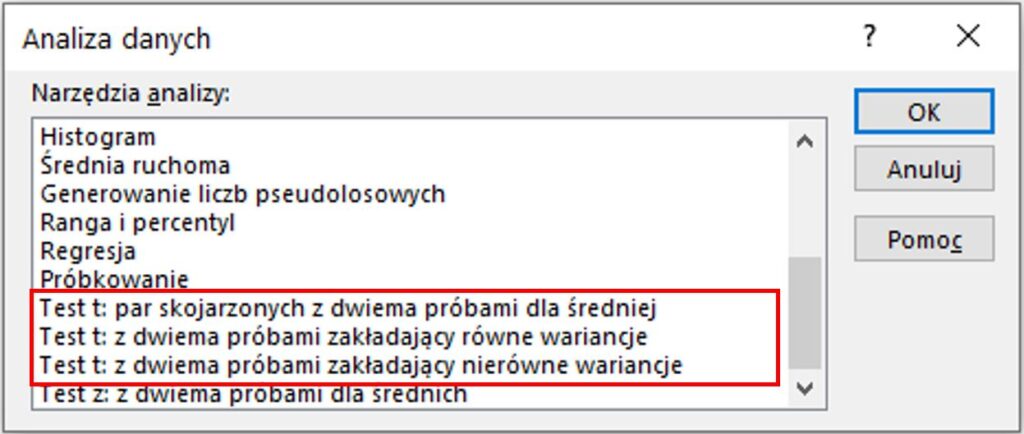
Przesuwając suwakiem w dół, testy t-Studenta znajdują się w dolnej części okna. Po wybraniu odpowiedniego testu otworzy się okno do wprowadzenia danych i wybrania miejsca przedstawienia wyniku analizy.
Z wykorzystaniem tego dodatku wykonano obliczenia zadań przedstawione poniżej.
PRAKTYKA
Zadanie 1: Test t dla prób niezależnych (równe wariancje)
Czy na podstawie przeprowadzonych pomiarów (wyniki na Rys. 3) można przyjąć, że stal węglowa o zawartości węgla 0,2% charakteryzuje się niższą granicą plastyczności Re [MPa] od staliwa węglowego o tej samej zawartości węgla?
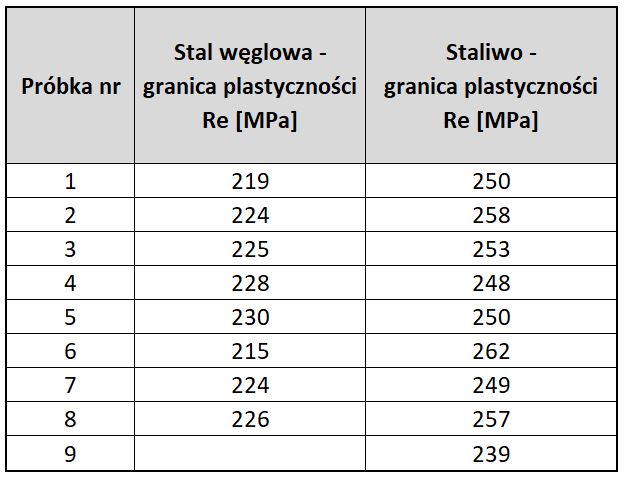
Wartości badanej cechy wyrażone są w skali ilorazowej. W wyniku testu normalności rozkładu otrzymano informację o przyjęciu H0 (brak podstaw do odrzucenia hipotezy o normalności rozkładów). Test t poprzedzono testem F dla wariancji. Wynik przedstawiono na Rys. 4.
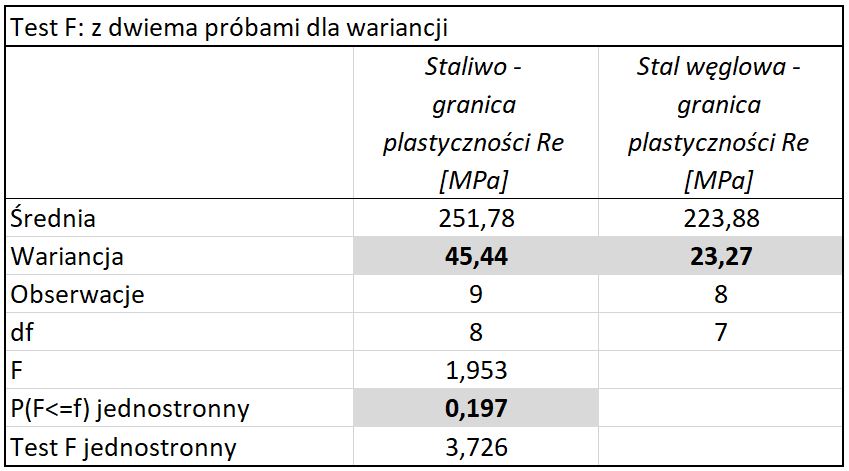
Ponieważ p-value 0,197 > α0,05 stwierdzono brak podstaw do odrzucenia hipotezy o jednakowych wariancjach. Do porównania średniej granicy plastyczności stali i staliwa zastosowano klasyczny test t-Studenta dla dwóch średnich – Rys.5.
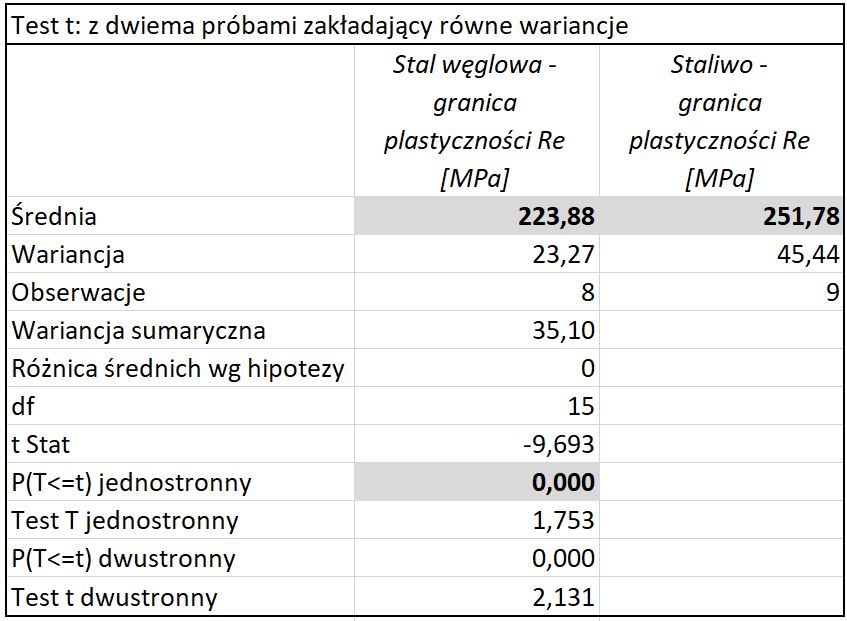
Ponieważ p-value 0,000 < α0,05 hipotezę zerową o jednakowej średniej granicy plastyczności stali i staliwa należy odrzucić. Stal węglowa o zawartości 0,0% węgla ma istotnie niższą granicę plastyczności.
Rozkłady pomiarów przedstawiono na dostępnym w programie MS Excel wykresie skrzynka-wąsy (ang. Box-Plot) Rys. 6. Na wykresie widoczne jest wyraźne przesunięcie rozkładu granicy plastyczności staliwa w stronę wartości wyższych w porównaniu do granicy plastyczności stali.
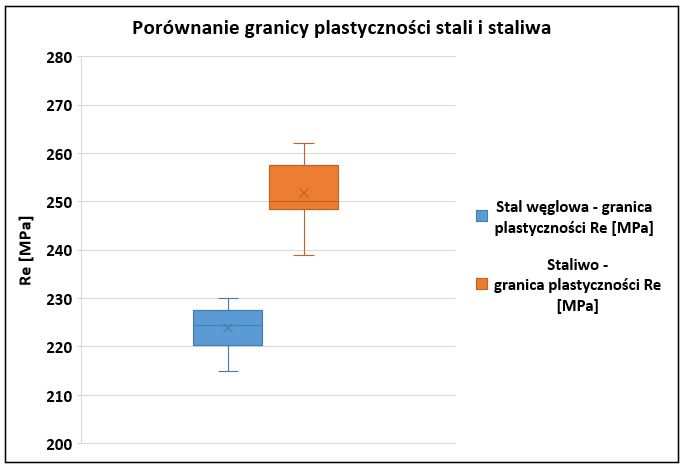
Zadanie 2: Test t dla prób niezależnych (nierówne wariancje)
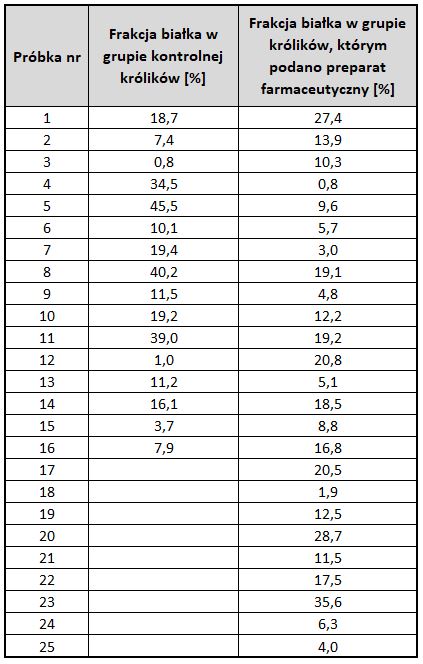
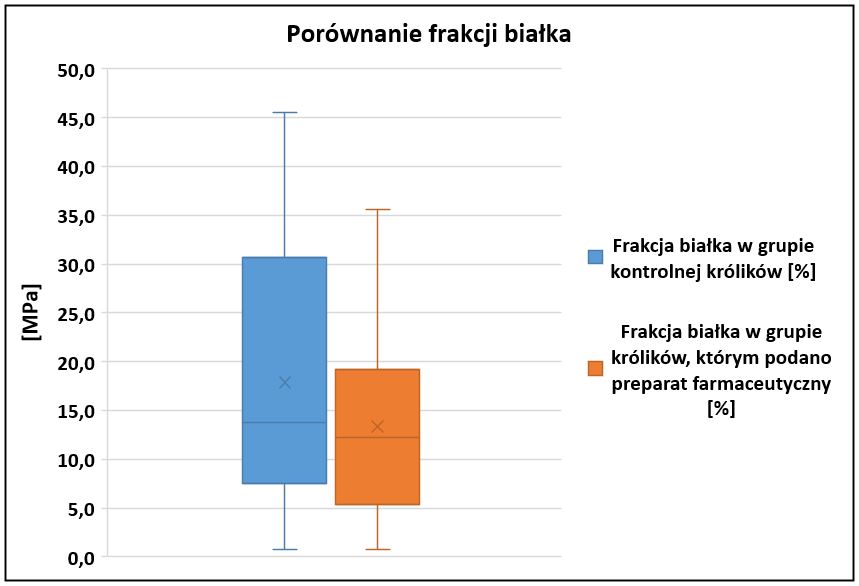
W celu stwierdzenia, czy podanie pewnego preparatu farmaceutycznego zmienia frakcję pewnego białka w moczu królików, dokonano 16 pomiarów frakcji tego białka w grupie kontrolnej królików oraz 25 pomiarów w grupie królików, którym podano badany preparat farmaceutyczny. Wyniki pomiarów przedstawiono na Rys. 7.
Na poziomie istotności statystycznej α0,05 zweryfikować hipotezę, że średnie frakcje badanego białka w moczu królików, którym nie podano preparatu i królików, które go otrzymały są identyczne.
Wartości badanej cechy wyrażone cechy są w skali ilorazowej. W wyniku testu normalności rozkładu otrzymano informację o przyjęciu H0 (brak podstaw do odrzucenia hipotezy o normalności rozkładów). Test t poprzedzono testem F dla wariancji. Wynik przedstawiono na Rys. 8.
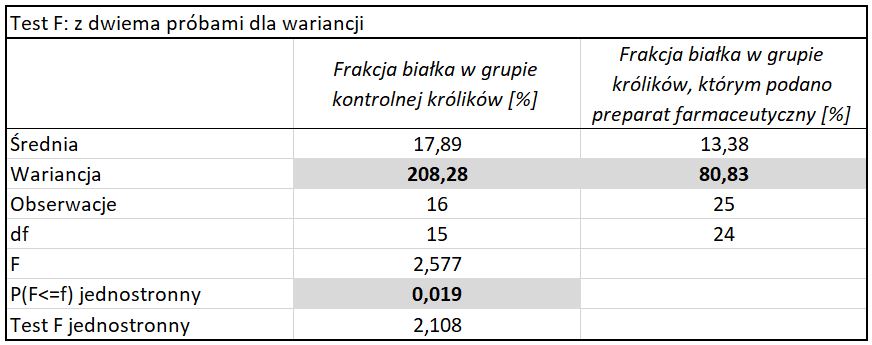
Ponieważ p-value 0,019 < α0,05 hipotezę zerową o jednakowych wariancjach odrzucono. Do porównania średnich frakcji białka w moczu królików zastosowano test t-Studenta przy nierównych wariancjach z poprawką Satterwhite’a. Wynik testu przedstawiono na Rys. 9.
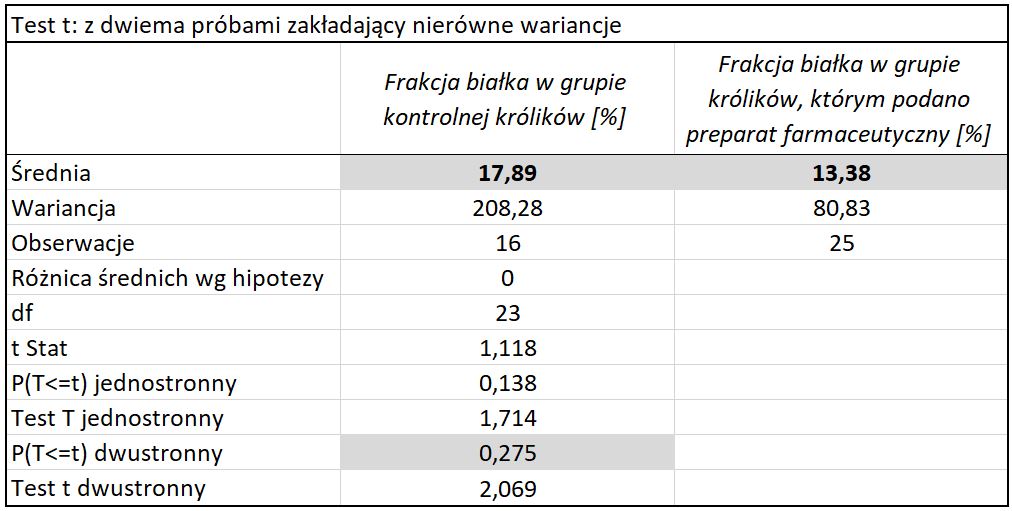
Ponieważ p-value 0,275 > α0,05 stwierdzono brak podstaw do odrzucenia zerowej. Przyjęto, że średnie frakcje badanego białka w moczu królików obydwóch grup są równe (nieistotnie różne).
Rozkłady pomiarów przedstawiono na wykresie skrzynka-wąsy na Rys. 10. Na wykresie widoczna jest nieznaczna różnica wartości średnich arytmetycznych obydwóch prób. Różnica jest na tyle niewielka, że za pomocą testu t nie udało wykazać się istotności statystycznej.
Zadanie 3: Test t dla par skojarzonych – próby zależne
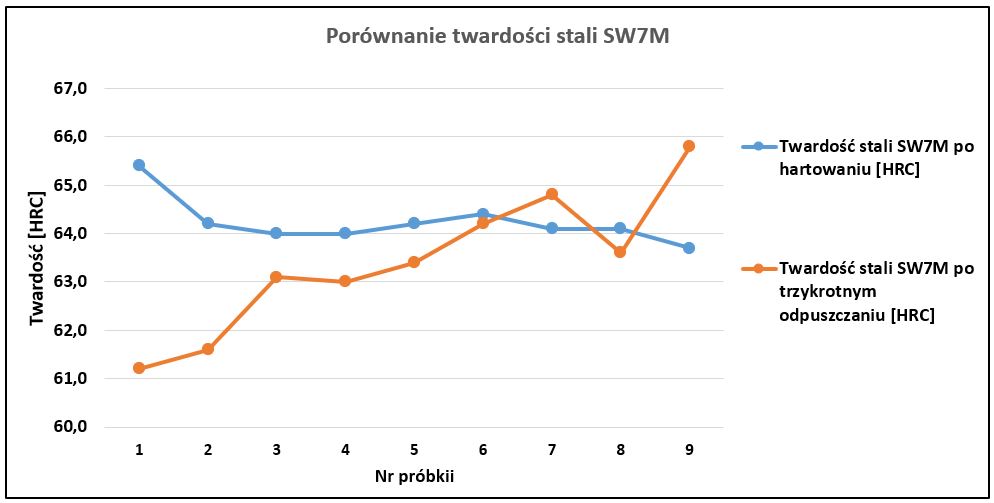
Sprawdzić, czy zastosowanie trzykrotnego odpuszczania stali szybkotnącej SW7M istotnie obniża twardość uzyskaną bezpośrednio po hartowaniu z zakresu temperatur 1170-1230 stopni C. Wyniki pomiarów twardości po hartowaniu i trzykrotnym odpuszczaniu przedstawiono na Rys. 11. Zweryfikować hipotezę na poziomie istotności α0,05.

W tym przypadku użyto testu t dla par skojarzonych, ponieważ każda próbka stali mierzona była dwukrotnie: pierwszy raz po hartowaniu i drugi raz po trzykrotnym odpuszczaniu stali. W ten sposób powstały pary skojarzone, czyli pary połączone sparowanymi wynikami pomiaru.
Hipotezę zerową sformułowano jako brak wpływu trzykrotnego odpuszczania próbek stali na spadek twardości, czyli że średnia różnica Zśr dwóch serii pomiarowych = 0.
Natomiast hipoteza alternatywna H1 miała brzmienie: Zśr < 0 – istotny spadek twardości po trzykrotnym odpuszczaniu (lewostronny obszar krytyczny).
Wynik obliczeń przedstawiono na Rys. 12.

Ponieważ p-value 0,104 > α0,05 (wartość statystyki t znalazła się poza lewostronnym obszarem krytycznym), należy stwierdzić brak podstaw do odrzucenia H0, zakładającej, że trzykrotne odpuszczanie nie powoduje obniżenia twardości stali szybkotnącej SW7M w stosunku do tej, jaką uzyskano bezpośrednio po zabiegu hartowania. Nie potwierdzono istotnego spadku twardości stali po trzykrotnym odpuszczaniu.
Rozkład analizowanych prób przestawiono na dostępnym w programie MS Excel wykresie liniowym – Rys. 13. Wykres nie przedstawia pełnej separacji prób. Widoczny jest pewien trend dla próbki po trzykrotnym odpuszczaniu, którego przyczynę powstania należałby sprawdzić dokładniej.
Zadanie 4: Test t dla par skojarzonych – próby zależne
Dane przedstawione na Rys. 14 prezentują oceny efektywności pracy menedżerów przed i po ukończeniu kursu zarządzania. Czy istnieje dowód na to, że kurs ten jest przydatny? Zweryfikować hipotezę na poziomie istotności α0,05.

Wartości badanej cechy (1 próba, 2 serie pomiarów tej samej cechy wynikowej) są ocenami przyznanymi wg nieokreślonej dokładnie skali. W zadaniu tym należy zweryfikować hipotezę o skuteczności kursu zarządzania, czyli średnią różnicę ocen po i przed wykonaniem kursu przez menedżerów.
Zadanie to rozwiązać można z wykorzystaniem dwóch testów: parametrycznego testu t-Studenta dla par skojarzonych lub nieparametrycznego testu rangowanych znaków Wilcoxona.
Test t-Studenta wymaga normalności rozkładu badanej cechy, czego jednoznacznie nie można określić z powodu trudności z ustaleniem skali pomiarowej. Z tego powodu korzystniej byłoby dokonać obliczeń z wykorzystaniem testu rangowanych znaków Wilcoxona. Test ten nie jest jednak dostępny w zautomatyzowanym dodatku Analysis ToolPak, więc obliczeń dokonano (po weryfikacji normalności rozkładu prób), wykorzystując test t-Studenta dla par skojarzonych – Rys. 15.
Hipoteza zerowa: brak wpływu ukończenia kursu na wzrost kompetencji menedżerów (średnia różnica Zśr dwóch serii pomiarowych = 0).
Hipoteza alternatywna H1: Zśr > 0 – istotny wzrost kompetencji menedżerskich po odbyciu kursu (prawostronny obszar krytyczny).

Ponieważ p-value 0,004 < α0,05, hipotezę zerową należy odrzucić. Potwierdzono istotny wzrost kompetencji menedżerskich po ukończonym kursie. Kurs zarządzania spowodował, że praca menedżerów jest efektywniejsza.
Rozkład analizowanych prób przestawiono na wykresie liniowym – Rys. 16. Wykres przedstawia istotną separację prób: dla 20 menedżerów nastąpił wzrost liczby punktów a tylko dla 5 spadek ocen.

PODSUMOWANIE
Testy t-Studenta chociaż są bardzo popularne, mają jednak ograniczenia.
Pierwszym ograniczeniem jest normalność rozkładu populacji, z których pobrano próby do testu. W przypadku niespełnienia tego warunku, szczególnie jeżeli populacje charakteryzują się dużą asymetrią, korzystanie z testów t-Studenta nie jest wskazane. W takim przypadku należy rozważyć inne opcje, między innymi testy nieparametryczne tj. test Manna-Whitneya, Mediany (Mood’s) czy Wilcoxona.
Drugim odgraniczeniem, w przypadku prób niezależnych jest jednorodność wariancji w analizowanych próbach, w związku z czym, przed wykonaniem testu t, należy wykonać test dla wariancji i na podstawie jego wyniku, dokonać wyboru odpowiedniego testu t dla prób niezależnych.
Należy pamiętać, że wynikiem testowania jest uzyskanie informacji o istotności statystycznej na podstawie wartości p-value. Nie jest to jednak miara efektu, dlatego oprócz istotności statystycznej należy także dokonać oceny efektu dla poszczególnych testów statystycznych. Można to zrobić obliczając i analizując dodatkowo wskaźniki efektu tj.: d Cohena, g Hedges’a czy Δ Glassa i inne.
Zadania wykorzystane w artykule zaczerpnięte zostały z książki: Weryfikacja hipotez statystycznych wspomaganych komputerowo, Marian Maliński, Gliwice 2004.
.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to udostępnij go w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
