Korelacja w procesie rozwiązywania problemów

Korelacja w procesie rozwiązywania problemów. Kluczowym etapem jest identyfikacja czynników (zmiennych objaśniających X), które wpływają w sposób istotny na zmienność oraz położenie analizowanego procesu (zmienna objaśniana Y).

W przypadku problemów trudnych, wieloczynnikowych, dotyczących zautomatyzowanych procesów produkcyjnych generujących dużą ilość danych, wykorzystywanie wielowymiarowej analizy korelacji przynosi korzyści w postaci redukcji czasu rozwiązywania problemu a w konsekwencji redukcję kosztów.

Analiza korelacji jest też bardzo dobrym wstępem do optymalizacji procesów z wykorzystaniem empirycznych i planowanych eksperymentów (DoE).

Korelacja – trochę teorii na ten temat…

Analiza współzależności

Dział statystyki, zajmujący się badaniem związków zachodzących między zmiennymi, którego celem jest odpowiedź na pytania:

• Czy między badanymi zmiennymi zachodzą istotne zależności?
• Jaka jest siła zależności?
• Jaki jest kierunek tych zależności?

Badając zależność między zmiennymi należy zwrócić uwagę na fakt, że badanie to ma sens tylko wtedy, kiedy między zmiennymi istnieje więź przyczynowo skutkowa, dająca się logicznie wytłumaczyć.

Siła i kierunek zależności

W celu określenia stopnia i kierunku zależności między badanymi zmiennymi można posłużyć się:

•  Współczynnikami korelacji.
•  Funkcją regresji.

Dwa podejścia:

• Jakościowe, czyli najpierw logiczne uzasadnienie występowania związku.
• Ilościowe, czyli analiza ilościowej zależności pomiędzy zmiennymi.

W praktyce wyróżnić można:

• Zależności dwustronne (trudno określić co jest skutkiem a co przyczyną), np.: relacja pomiędzy wydatkami na reklamę a zyskiem w przedsiębiorstwie – im większe wydatki na reklamę, tym większy zysk, jednakże poziom osiągniętego zysku wpływa na zwiększenie funduszu przeznaczonego na reklamę.
• Zależności jednostronne – jednokierunkowe oddziaływanie przyczyny na skutek, np.: wiek samochodu wpływa na jego cenę.

Ilościowa analiza współzależności obejmuje:

• Analizę korelacji, czyli pomiar siły i kierunku zależności pomiędzy cechami.
• Analiza regresji, czyli badanie mechanizmu powiązań pomiędzy cechami, którego wyrazem są funkcje regresji.

Analizę korelacji wykonać można z wykorzystaniem statystycznych metod, które użyte mogą być w stosunku do danych wyrażonych w skali ilościowej lub jakościowej.

Współczynnik korelacji

Jest miernikiem siły i kierunku zależności korelacyjnej między zmiennymi. Zależność korelacyjna – charakteryzuje się tym, iż określonym wartościom jednej zmiennej przyporządkowane są ściśle określone wartości drugiej zmiennej.

Kierunek zależności:

• Brak zależności, gdy wartość współczynnika korelacji = 0
• Zależność dodatnia (pozytywna), gdy wartość współczynnika korelacji > 0.
• Zależność ujemna (negatywna), gdy wartość współczynnika korelacji < 0.

Siłę zależności (przyjęto umownie) można wyrazić w formie liczbowej wartości współczynników zawartych w przedziale od -1 do 1, gdzie odpowiednia wartość dla korelacji dodatniej oznacza:

• r_xy < 0,2 – praktycznie brak związku pomiędzy cechami.
• 0,2 < r_xy < 0,4 – zależność (korelacja) widoczna, ale słaba.
• 0,4 < r_xy < 0,7 – zależność umiarkowana.
• 0,7 < r_xy < 0,9 – zależność silna, znacząca.
• r_xy > 0,9 – zależność bardzo silna.

Analogicznie dla korelacji ujemnej:

• r_xy > – 0,2 – praktycznie brak związku pomiędzy cechami.
• – 0,2 > r_xy > – 0,4 – zależność (korelacja) widoczna, ale słaba.
• – 0,4 > r_xy > – 0,7 – zależność umiarkowana.
• – 7 > r_xy > – 0,9 – zależność silna, znacząca.
• r_xy < – 0,9 – zależność bardzo silna.

Test istotności dla współczynnika korelacji:

Określenie „korelacja słaba bądź silna” jest jedynie orientacyjne, ponieważ oprócz tych określeń należy udzielić odpowiedzi na pytanie czy korelacja jest istotnie różna od zera.

W tym celu za pomocą testu istotności statystycznej dla współczynnika korelacji należy zweryfikować hipotezę:

H0:  r = 0 – korelacja jest nieistotna statystycznie.

H1: r ≠ 0 – korelacja jest istotna statystycznie.

Po obliczeniu wartości współczynnika korelacji z próby, następnie należy wyznaczyć wartość statystyki t wg wzoru:

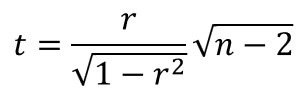
która przy założeniu prawdziwości H0 (hipotezy zerowej) posiada rozkład t-Studenta o liczbie stopni swobody równej n-2.

Oblicza się wartość prawdopodobieństwa p-value, jeśli zajdzie relacja:

• p-value > α (najczęściej 0,05) to nie ma podstaw do odrzucenia H0 i stwierdza się brak istotnej korelacji pomiędzy zmiennymi.
• p-value ≤ α to H1 (hipoteza alternatywna) jest akceptowana, co oznacza, iż korelacja pomiędzy zmiennymi jest istotna statystycznie.

W przypadku danych ilościowych wyrażonych za pomocą liczb najczęściej wykorzystywane są współczynniki korelacji:

• Pearsona dla ilościowych zależności liniowych pomiędzy zmiennymi.
• Spearmana to współczynnik korelacji rang, tzw. współczynnik korelacji kolejnościowej.

Korelacja Pearsona – statystyka współczynnika przedstawia się następująco:

.

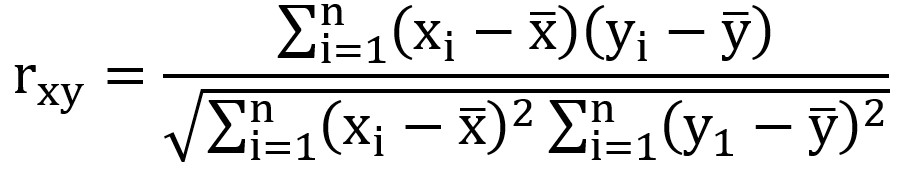
Przykład wykorzystania współczynnika korelacji Pearsona:

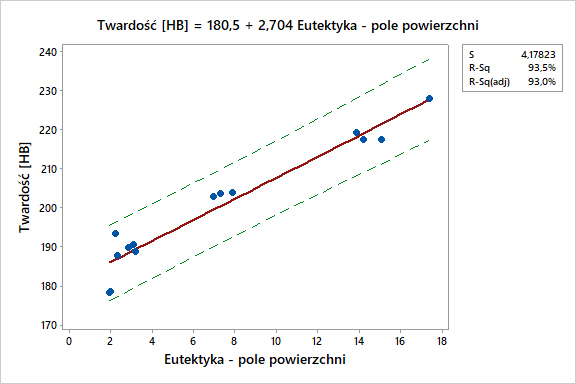
Dane w tabeli na rys. 1 przedstawiają zależność pomiędzy eutektyką fosforową w żeliwie a twardością żeliwa zmierzoną metodą pomiarów twardości Brinella. Na podstawie danych określić należy siłę, kierunek oraz istotność statystyczną zależności pomiędzy dwoma zmiennymi niezależnymi wyrażonymi w skali ilościowej.

Wynik analizy:

Współczynnik korelacji Pearsona wyniósł 0,97, czyli bardzo silną i dodatnią korelację: wraz ze wzrostem pola powierzchni eutektyki w strukturze żeliwa, wzrasta jego twardość. Wartość prawdopodobieństwa p-value wyniosła 0,00, co potwierdza H1: korelacja pomiędzy ilością eutektyki a twardością żeliwa jest istotna statystycznie.

Wniosek:

W celu zwiększenia twardości żeliwa, należy doprowadzić do sytuacji, w której jego struktura zawierać będzie większy udział eutektyki.

Uwaga!:

Przedstawianie wartości współczynnika korelacji bez wykresu jest poważnym błędem i w skrajnych przypadkach prowadzić może do błędnego wnioskowania. Zależność pomiędzy zmiennymi zawsze powinna być przedstawiona również graficznie np.: z wykorzystaniem wykresu punktowego (ang. Scatterplot) rys.2.

Korelacja rang Spearmana – współczynnik:

Współczynnik korelacji kolejnościowej (współczynnik korelacji rang) wykorzystywany jest w przypadku gdy:

• Dane mają rozkład inny niż normalny.
• Cechy mają charakter jakościowy lecz istnieje możliwość ich uporządkowania.

Statystyka współczynnika korelacji rang Spearmana:

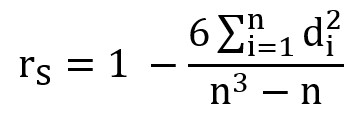
Gdzie di jest różnicą rang R(xi) – R(yi).

Potwierdzenie istotności statystycznej wyznaczane jest tak, jak w przypadku korelacji Pearsona.

Przykład wykorzystania współczynnika korelacji Spearmana:

Dział marketingowy firmy krawieckiej podjął badania, których celem było ustalenie korelacji pomiędzy wielkością sprzedaży garniturów a ich typem. Analizie poddano 10 typów garniturów, w odniesieniu do których wyznaczono 4-stopniową skalę „atrakcyjności wyglądu”, w punktach: 1 (niemodny), 2 (praktyczny), 3 (modny), 4 (super modny). Dokonać należy oceny czy istnieje pozytywna korelacja pomiędzy typem garnituru a wielkością sprzedaży. Dane przedstawiono w tabeli na rys.3.

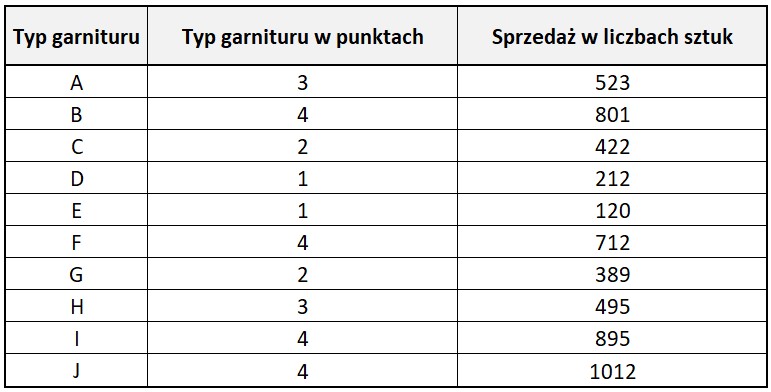
Wynik analizy:

Współczynnik korelacji Spearmana wyniósł 0,96, czyli bardzo silną i dodatnią korelację. Wartość prawdopodobieństwa p-value wyniosła 0,00, co potwierdza H1: korelacja pomiędzy typem garnituru a wielkością sprzedaży jest istotna statystycznie.

Wniosek:

W celu zwiększenia sprzedaży garniturów należy skupić się na produkcji i sprzedaży garniturów „super modnych”.

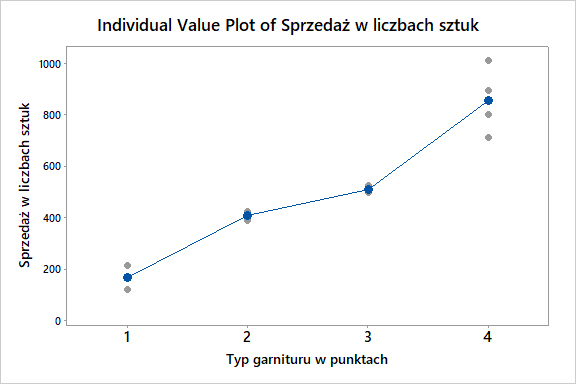
W tym przypadku dobrym wykresem w celu graficznej analizy danych będzie wykres wartości indywidualnej (ang. Individual Value Plot) przedstawiony na rys.4.

Miary zależności cech jakościowych

Gdy zachodzi konieczność ustalenia zależności pomiędzy cechami niemierzalnymi lub pomiędzy zmienną jakościową i mierzalną i każda ze zmiennych niemierzalnych ma dwa warianty (podział dychotomiczny) to zaobserwowane liczebności można przedstawić w postaci czteropolowej tablicy (rys.5):

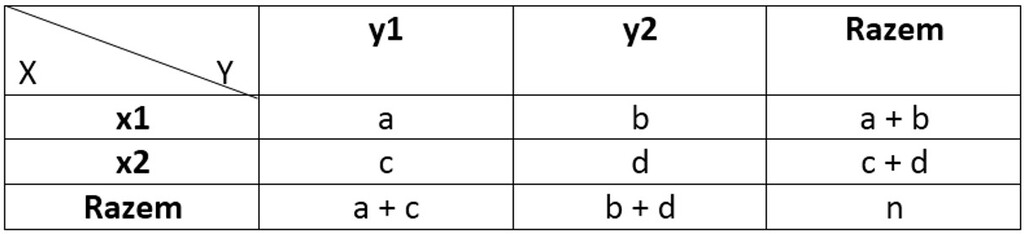
Symbolami a, b, c, d oznaczono absolutne (lub procentowe) liczebności jednostek mające określone warianty cech.

Do pomiaru siły zależności pomiędzy badanymi cechami wykorzystuje się tzw. współczynniki zbieżności korelacyjnej:

• Pearsona-Bravaisa.
• Bykowskiego.
• Yula-Kendalla.

Test Niezależności χ2:

Test stosuje się w celu zbadania zależności pomiędzy dwoma zmiennymi, które wyrażone mogą być w skalach:

• Mierzalnych, czyli co najmniej skala różnicowa.
• Jakościowych, czyli skala nominalna lub porządkowa.

Test niezależności pozwala na zweryfikowanie hipotezy H0, iż badane cechy są niezależne.

Losowana jest n elementowa próba a zaobserwowane w próbie wartości cech x i y zapisywane w tablicy korelacyjnej o wymiarach r * k. Sprawdzianem testu jest statystyka:

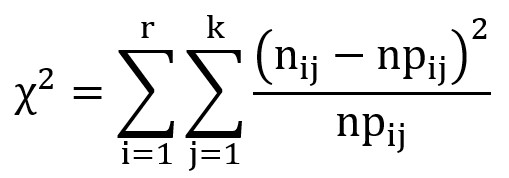
Gdzie:

• n_ij – liczebność empiryczna w macierzy liczebności:

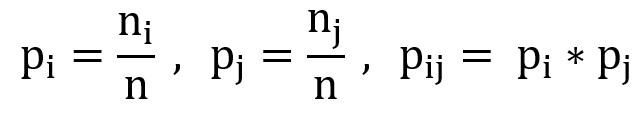
Gdzie:

• n_i – suma liczebności w i-tym wierszu.
• n_j – suma liczebności w j-tej kolumnie.

Powyższa statystyka ma przy założeniu prawdziwości H0 asymptotyczny rozkład χ2 o (r-1)(k-1) stopniach swobody.

W przypadku danych, dla których poziomy czynnika wyrażone są w skali nominalnej na wielu poziomach wykorzystuje się tablice wielopolowe.

Przykład wykorzystania testu niezależności χ2:

Analityk hurtowni napojów orzeźwiających postanowił przeprowadzić analizę czy istnieje związek pomiędzy preferencjami konsumentów w stosunku do 4 popularnych napojów a ich odpowiednikiem w wersji zwykłej i dietetycznej (tzw. light). Analizę wykonano na podstawie próby losowej o liczebności 3253 osób. Wynik przedstawiono w tabeli na rys. 6.

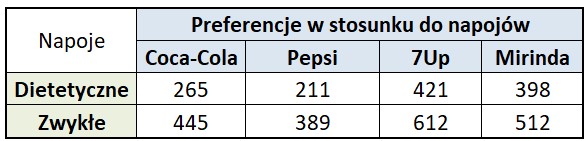
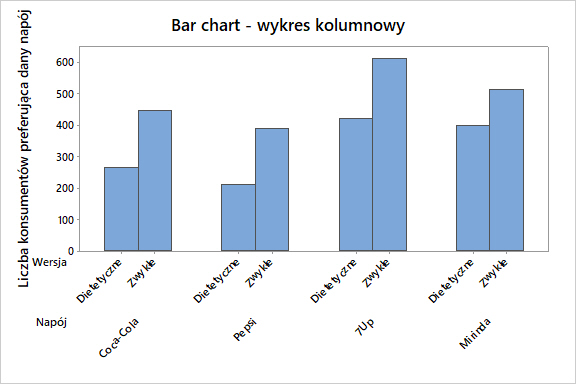
W wyniku analizy nie potwierdzono niezależności pomiędzy zmiennymi. Na podstawie statystyki χ2 (13,47) policzono wartość prawdopodobieństwa p-value (0,004) i stwierdzono, iż istnieje zależność pomiędzy preferencjami konsumentów a popularnymi napojami w wersji zwykłej i dietetycznej. Statystycznie, bez względu na typ napoju konsumenci wybierają ich wersje „zwykłe” częściej niż wersje „dietetyczne”. Na rys. 7. graficznie przedstawiono wynik analizy.

Przykład praktyczny analizy korelacji dla wielu zmiennych objaśniających

Wykorzystanie analizy korelacji w procesie rozwiązywania problemów jest czynnością kluczową w sytuacji, w której zbierane są dane z wykorzystaniem np. arkusza kontrolnego.

Tabela na rys. 8. przedstawia dane zbierane przez osobę odpowiedzialną za programowanie elektrycznych wkrętarek dokręcających sterowanych elektronicznie w Firmie produkującej wyroby z wykorzystaniem technologii połączeń gwintowych.

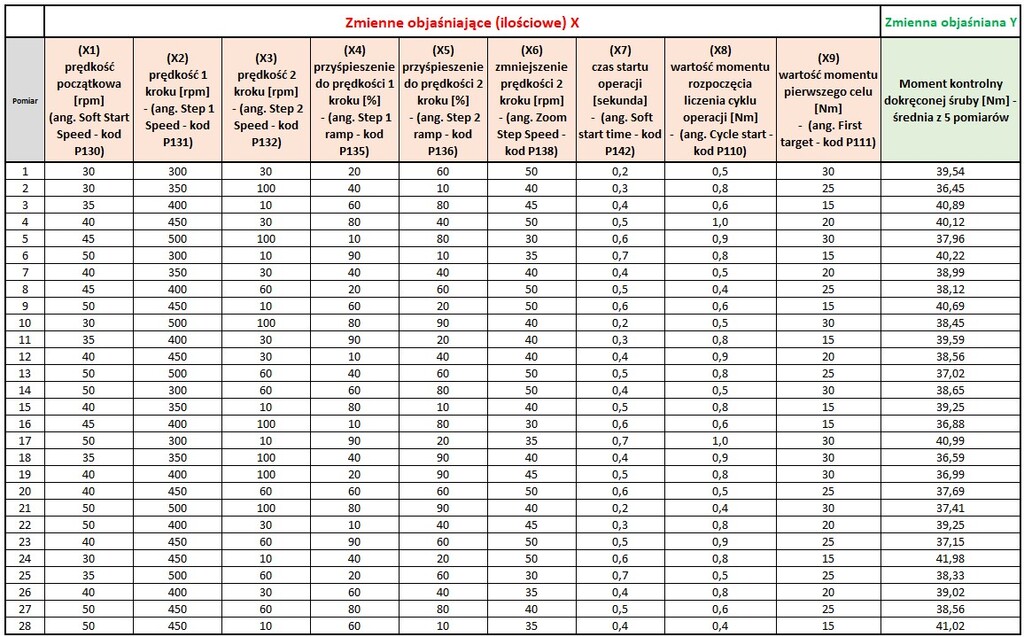
W tabeli na rys. 8. znajdują się wartości dziewięciu zmiennych objaśniających X (nastawy programu dokręcającego sterownika wkrętarki) rejestrowane w sposób nieuporządkowany oraz wartości zmiennej objaśnianej Y (pomiary momentów kontrolnych śrub z wykorzystaniem ręcznego narzędzia dynamometrycznego typu 1).

Osoba „zbierająca” dane nie posiadała wiedzy z zakresu planowania eksperymentów (DoE), natomiast znała i wykorzystywała analizę korelacji pomiędzy zmiennymi. Stąd ten nieuporządkowany (brak planu) wygląd tabeli.

Problemem w tym procesie była zbyt niska w porównaniu do momentu dokręcania, wartość momentu kontrolnego. Celem rozwiązania tego problemu było przesunięcie rozkładu pomiarów momentu kontrolnego w stronę wartości wyższych.

Mając do dyspozycji tabelę z tak przygotowanymi danymi, jeszcze przed „oficjalnym” rozpoczęciem procesu rozwiązywania tego problemu (nie będąc nawet w punkcie D1 metody G8D), można w ciągu kilkudziesięciu sekund zdobyć istotną wiedzę, którą wykorzystać można będzie na dalszym etapie rozwiązywania problemu.

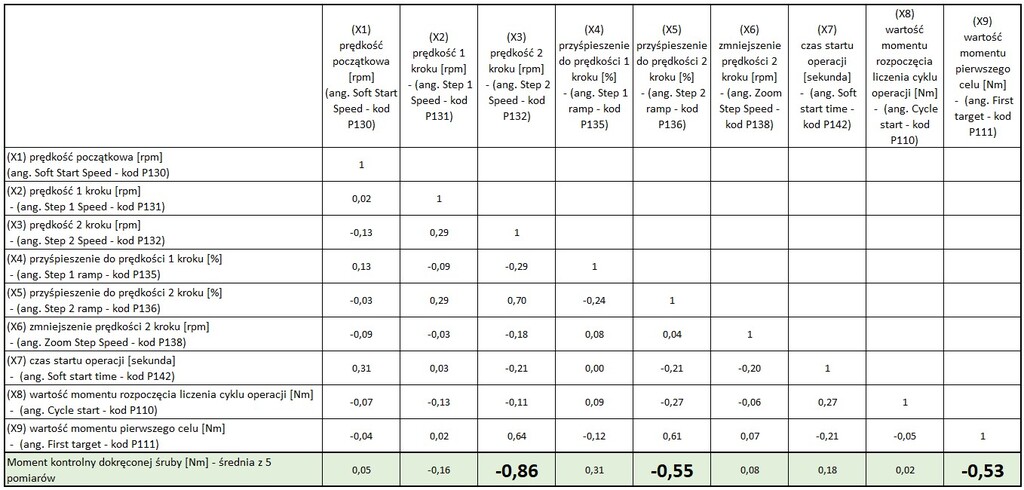
Na przykład w programie MS Excel, idąc do zakładki „Dane – Analiza Danych – Korelacja„ można przygotować tabelę z wartościami współczynników korelacji Pearsona dla danych z tabeli przedstawionej na rys. 8. Tabelę z wartościami współczynników korelacji przedstawiono na rys. 9. Wiersz zawierający dane dla zmiennej Y oznaczono kolorem zielonym.

Zależności pomiędzy zmiennymi objaśniającymi X a zmienną objaśnianą Y pokazano także na zbiorczym wykresie punktowym (rys. 10).

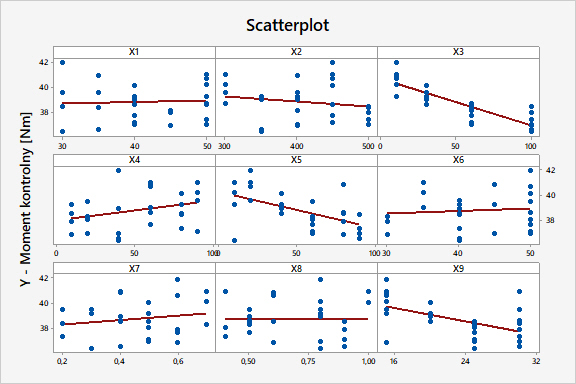
Wnioski:

• Potwierdzono silną korelację ujemną (-0,86) pomiędzy czynnikiem X3 a zmienną Y: wraz ze wzrostem prędkości dokręcania [rpm] w kroku drugim, spada wartość momentu kontrolnego [Nm].
• Potwierdzono także umiarkowaną korelację ujemną pomiędzy czynnikiem X5 (-0,55) oraz X9 (-0,53) a zmienną Y.
• Stwierdzono także występowanie korelacji pomiędzy zmiennymi objaśniającymi (np.: X3 i X5 – współczynnik korelacji wynosi 0,70), co z punktu widzenia prowadzenia analizy z wykorzystaniem planowanego eksperymentu (DoE) lub analizy regresji wielorakiej nie jest dobrą informacją – zmienne X nie powinny być skorelowane.
• Jeżeli na dalszym etapie rozwiązywania problemu podjęta zostanie decyzja o wykonaniu eksperymentu empirycznego (DoE), to w pierwszej kolejności analizie poddane zostaną zmienne objaśniające: X3, X5, X9.

Podsumowanie

Wykorzystanie analizy korelacji w procesie rozwiązywania problemu lub optymalizacji procesów produkcyjnych jest zabiegiem opłacalnym z punktu widzenia identyfikacji przyczyny / przyczyn powstawania problemów.

Budując i wykorzystując arkusze kontrolne do zbierania danych, należy zawsze mieć na uwadze możliwość zmierzenia siły korelacji pomiędzy zapisywanymi danymi, a prawidłowa ocena i interpretacja tych danych w każdym przypadku ułatwia i skraca czas procesu rozwiązywania problemów.

Analizę korelacji można w sposób prosty i szybki przeprowadzić wykorzystując program MS Excel lub Minitab.

Autor: dr inż. Rafał Popiel

Jeżeli artykuł Ci się podobał, to udostępnij go w mediach społecznościowych:

• LinkedIn
• Facebook
• Instagram

Zaufali nam:

.

Co mówią nasi zadowoleni Klienci:

.

W przypadku pytań zapraszamy do kontaktu: