Test równoległości dwóch regresji prostych

W niniejszym artykule przedstawiono sposób wykorzystania testu równoległości dwóch regresji prostych w procesie połączeń gwintowych.
Test ten umożliwia porównanie dwóch współczynników regresji (równoległość prostych). Koncepcyjnie zgodny jest z testem dla dwóch średnich arytmetycznych. Wartość statystyki t oblicza się wg wzoru:
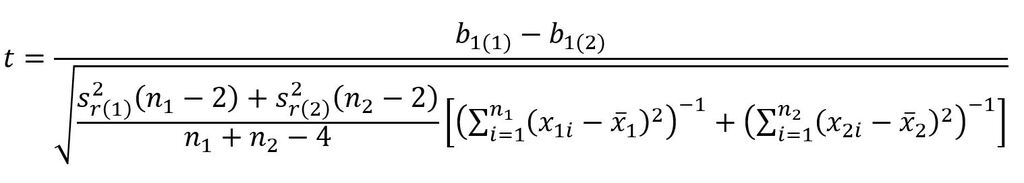
Gdzie:
b1(1) i b1(2) – to estymatory kierunkowych współczynników regresji,
s2r(1) i s2r(2)– to estymatory wariancji resztowych,
n1 i n2 – to liczebności obydwóch prób.
Przy założeniu prawdziwości H0, która zakłada równoległość obu linii regresji β1(1) = β1(2) statystyka t ma rozkład t-Studenta o liczbie stopni swobody n1+n2-4.
Praktyczne zastosowanie testu
Test został wykorzystany przy ocenie jakości dokręcania (porównaniu) dwóch rodzajów śrub. Każda śruba pochodziła od różnego dostawcy.
Śruby charakteryzowały się tą samą klasą wytrzymałości 10.9.
Właściciel procesu dokręcania (do testów) dysponował tylko 2 sztukami śrub proponowanych, czyli takich, którymi chciano zastąpić śruby bieżące, które używane były w procesie od kilku lat.
Do celów analizy wykonano po jednym dokręceniu dla każdej śruby (bieżąca i proponowana) wykorzystując ręczne narzędzie dynamometryczne typu 1, które próbkowało wartość momentu dokręcania w stosunku do wartości kąta dokręcania (część pierwsza na Rys.1.).
Na podstawie powstałych punktów współrzędnych wykorzystując wykres dwupunktowy, zbudowano wykresy dla zakresów sprężystych dokręcania śrub. Do punktów dopasowano linie regresji prostych w celu zobrazowania ich wzajemnego położenia (Rys.2.).
Jeżeli linie regresji są względem siebie równoległe, założyć można że śruby od różnych dostawców zachowują się podobnie podczas dokręcania; tj. że wartość siły osiowej [kN] po osiągnięciu danego momentu dokręcenia [Nm] dla każdej śruby będzie bardzo zbliżona.
Obliczenia zgodne z powyższym wzorem przedstawiono w drugiej części na Rys.1.


Wynik analizy:
Na przedstawionym wykresie (Rys.2.) widoczny jest brak równoległości dwóch prostych regresji. Zostało to także potwierdzone statystycznie poprzez obliczenie wartości p-value, która była niższa niż przyjęty poziom istotności statystycznej α0,05.
W praktyce oznacza to, że wartości sił osiowych [kN] wygenerowanych dla takiej samej wartości momentu dokręcenia [Nm] dla każdej śruby będą różne.
W tym przypadku wartość współczynnika kierunkowego dla śruby proponowanej (0,366) jest niższa niż dla śruby bieżącej (0,563), co oznacza, że siła osiowa dla śruby proponowanej będzie wyższa. Jeżeli będzie na tyle wysoka, że wygenerowane naprężenie na rdzeń śruby [MPa] przekroczy granicę plastyczności śruby [Re] przed osiągnięciem momentu dokręcenia [Nm], to doprowadzi to do ukręcenia (zerwania) śruby podczas operacji dokręcania.
Wnioski z analizy:
- Na podstawie wyniku analizy, na tym etapie procesu zmiany, wydano rekomendacje niewdrażania śrub proponowanych.
- Zaproponowano wykonanie dokładniejszej analizy, z wykorzystaniem próbki o większej liczności śrub bieżących i proponowanych oraz z użyciem elektrycznych wkrętarek dokręcających – szczegóły i posumowanie w innym artykule: Metoda prowadzenia analizy statystycznej podczas wprowadzania zmiany konstrukcyjnej elementu połączenia gwintowego.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
