Kluczowa rola statystyki opisowej w SPC

SPC
Nowoczesne i otwarte na zmiany przedsiębiorstwo, nastawione jest na sprawne funkcjonowanie systemu zarządzania jakością wyrobów i usług. Kluczową rolę w takim systemie odgrywa statystyczne sterowanie procesem (SPC).
Historyczne podejście do pojęcia jakości opierało się na utrzymaniu procesu (charakterystyk mierzonych produktu) w granicach tolerancji USL i LSL (ang. Upper / Lower Specification Limit) założonych przez konstruktora i oczekiwanych przez klienta.
Jednak wymagania rynku spowodowały, że do jakości procesu zaczęto podchodzić poprzez ciągłe jego doskonalenie: minimalizację wielkości rozrzutu (najczęściej estymując odchylenie standardowe) oraz centralizację do wartości docelowych procesu.
Ogólnie SPC można opisać jako realizowaną w bieżącym czasie kontrolę przebiegu procesu, mającą na celu identyfikację ewentualnych rozregulowań (pojawienie się zmiennej specjalnej) i stałej poprawie jakości procesu.
Stosując SPC, analizie poddaje się:
- Losowość procesu lub jego brak wskutek występowania zjawisk nielosowych (zmiennej specjalnej) tj. m.in.: trendy, mieszaniny, oscylacje, skupienia danych itp.
- Wielkość rozrzutu procesu, który nie może wykraczać poza granice specyfikacji (USL i LSL), ale również poza tzw. granice kontrolne / interwencji (UCL i LCL).
- Wycentrowanie procesu względem wartości docelowej.
MSA
Wykorzystując SPC w przedsiębiorstwie, nie należy zapominać o stosowaniu MSA (ang. Measurement System Analysis), czyli analizy systemów pomiarowych, która jest metodą badania zdolności i stabilności narzędzi i systemów pomiarowych.
Krótko mówiąc: rejestrując anomalie w procesie, należy mieć pewność, że te anomalie nie pochodzą od systemu pomiarowego.
Czy coś jeszcze należy wdrożyć do systemu jakości w celu prowadzenia SPC?
Tak!
Statystyka opisowa
Należy wdrożyć narzędzia statystyki opisowej, bowiem SPC zawiera wiele technik i narzędzi, które stosować należy w odniesieniu do konkretnego rozkładu zmiennej losowej, czyli analizowanej i mierzonej charakterystyki.
W warunkach produkcji przemysłowej można rozróżnić dwa rodzaje rozkładów zmiennej losowej: o charakterze ciągłym i dyskretnym (skokowym) – przedstawiono na Rys.1.
.
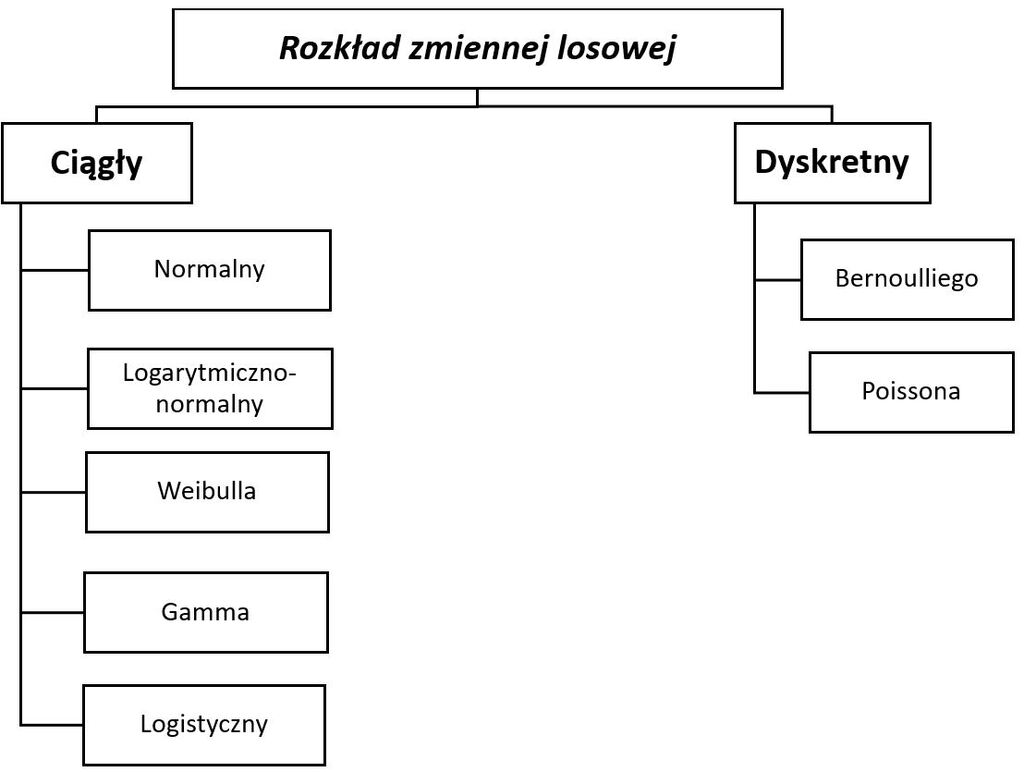
Zmienna losowa ma charakter ciągły, jeżeli jej wartości należą do przedziału ze zbioru liczb rzeczywistych np. wynik pomiaru 125,64 Nm. Natomiast zmienną losową dyskretną, jest zmienna, która ma skończony lub przeliczalny zbiór wartości, najczęściej ograniczony do liczb naturalnych.
Rozkład Normalny
Jednym z najważniejszych rozkładów prawdopodobieństwa zmiennej losowej typu ciągłego występującym w przemyśle jest rozkład normalny nazywany także rozkładem Gaussa.
Większość narzędzi SPC jest opracowanych właśnie dla tego rozkładu danych, w szczególności najbardziej popularne karty kontrolne Shewharta czy klasyczne wskaźniki zdolności procesu (Cp/Cpk) i wydajności procesu (Pp/Ppk).
Stosując klasyczne wskaźniki zdolności i wydajności procesu (w mianowniku wzorów liczony jest estymator odchylenia standardowego) dla charakterystyki, którą nie można opisać rozkładem Gaussa, należy liczyć się z istotnym błędem estymacji. Obliczone wartości wskaźników nie oddadzą rzeczywistej jakości procesu, a co za tym idzie, obliczone prawdopodobieństwo braków (pomiarów poza specyfikacją) będzie nieprawdziwe.
Przykład SPC z przemysłu: analiza wartości momentów dokręcania łącznika gwintowego.
Moment dokręcania wyrażany za pomocą jednostki Nm (niuton-metr) to zmienna losowa o charakterze ciągłym.
Wartości momentu dokręcania pobrać można ze sterowników zaawansowanych wkrętarek dynamometrycznych. Na Rys.2. przedstawiono wynik analizy rozkładu momentów dokręcania z dopasowaniem teoretycznego rozkładu normalnego.
.
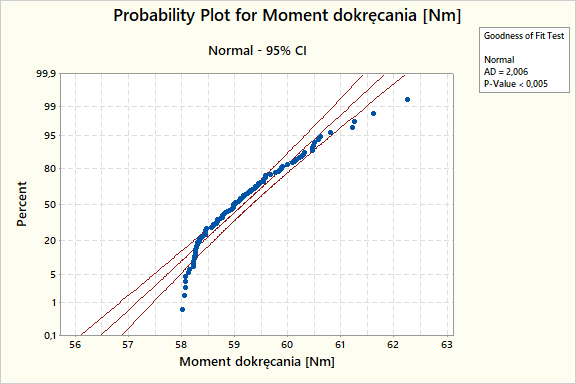
W wyniku analizy stwierdzono brak zgodności rozkładów:
- Niebieskie punkty (rozkład empiryczny wartości momentów dokręcania) nie pokrywa się z prostą rozkładu teoretycznego normalnego.
- Wartość p-value jest niższa, od przyjętego poziomu istotności statystycznej (α0,05) w związku z czym odrzucono H0 stanowiącą o zgodności rozkładu empirycznego i teoretycznego.
Dodatkowo policzono estymatory:
- Skośności rozkładu: 1,01 to rozkład o prawostronnej asymetrii.
- Kurtozy: 0,95 to rozkład leptokurtyczny.
Pp/Ppk
Wykonując analizę wydajności procesu z wykorzystaniem klasycznych wskaźników Pp i Ppk spodziewać się należy wyniku takiego, jaki przedstawiono na Rys.3.
.
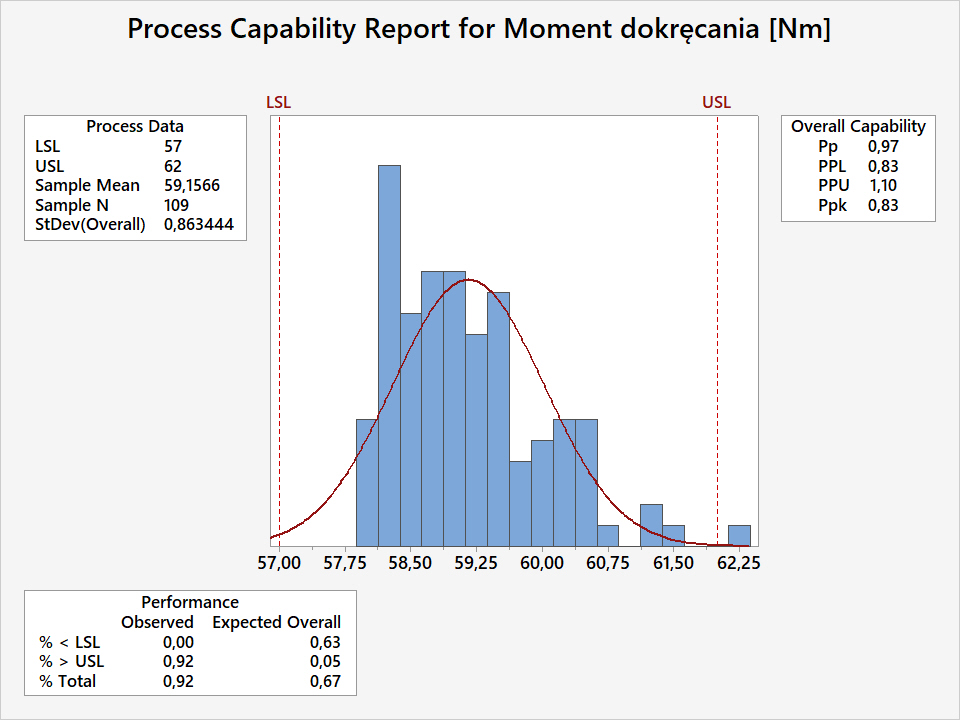
Ponieważ dopasowanie pomiarów momentu dokręcania rozkładem normalnym jest nieprawidłowe to wartości wskaźników PPL i PPU są zafałszowane.
Obliczone w ten sposób wskaźniki podają błędne wartości:
- PPL 0,83 – zbyt niską wartość.
- PPU 1,10 – zbyt wysoką wartość.
Przekłada się to na następującą estymację momentów dokręcania poza granicami tolerancji:
- Frakcja poniżej LSL wynosi 0,63%.
- Frakcja powyżej USL wynosi 0,05%.
Rozkład Gamma
Analizując natomiast zgodność rozkładu momentów dokręcania z teoretycznym rozkładem gamma, otrzymać można o wiele lepsze dopasowanie – Rys.3.
.

W wyniku analizy stwierdzono zgodność rozkładu momentów dokręcania z teoretycznym rozkładem gamma:
- Niebieskie punkty (rozkład empiryczny wartości momentów dokręcania) dosyć dobrze pokrywają prostą rozkładu teoretycznego gamma.
- Wartość p-value jest wyższa od przyjętego poziomu istotności statystycznej (α0,05), w związku z czym przyjęto H0 stanowiącą o zgodności rozkładu empirycznego i teoretycznego.
Dysponując tak dobrym dopasowaniem rozkładów, przeprowadzić można analizę wydajności procesu modelując teoretycznym rozkładem gamma. Na Rys4. przedstawiono wynik analizy.
.
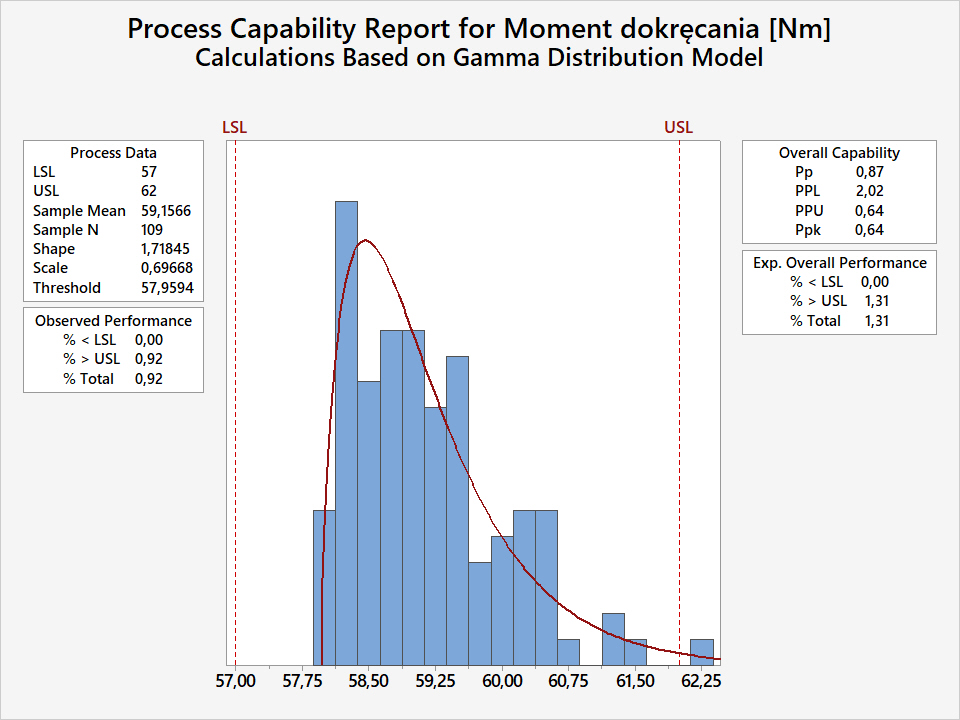
Ponieważ dopasowanie pomiarów momentu dokręcania rozkładem gamma jest prawidłowe, to wartości wskaźników PPL i PPU nie są zafałszowane. Obliczone w ten sposób wskaźniki podają zbliżone do rzeczywistości wartości:
- PPL 2,02.
- PPU 0,64.
Przekłada się to na następującą estymację momentów dokręcania poza granicami tolerancji:
- Frakcja poniżej LSL wynosi 0,00%.
- Frakcja powyżej USL wynosi 1,31%.
Porównanie i wnioski:
| Dopasowanie rozkładem: | Wskaźnik PPL | Wskaźnik PPU |
| Normalnym | 0,83 | 1,10 |
| Gamma | 2,02 | 0,64 |
Dążąc do poprawy jakości rozkładu momentów dokręcania i opierając się na obliczeniach opartych na rozkładzie normalnym, rozpoczęte zostałyby działania mające na celu poprawę lewej strony rozkładu (wartości niższe), podczas gdy lewa strona rozkładu nie stwarza zagrożenia z pkt. widzenia jakości procesu. Pominięto by (przynajmniej w pierwszej fazie) poprawę prawej strony rozkładu (wartości wyższe).
Byłoby to oczywiście błędne działanie, ponieważ obliczając wskaźniki z dopasowaniem poprawnego rozkładu gamma, otrzymano informację, że poprawa rozkładu momentów dokręcania powinna rozpocząć się od strony prawej, gdzie szacowana frakcja braków wynosi 1,31%.
Podsumowanie:
Statystyka opisowa jest kluczowym etapem w stosowaniu statystycznej kontroli procesu. Wykorzystując oferowane przez nią techniki analizy i estymacji podstawowych statystyk rozkładu analizowanych danych prowadzi do wyboru odpowiednich narzędzi SPC, a co za tym idzie podejmowania prawidłowych decyzji co do poprawy jakości procesu.
Wykorzystywanie statystyki opisowej powinno być integralną częścią SPC, bez której podejmowanie decyzji o jakości procesu jest ryzykowne.
.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
