Regulacja procesu z wykorzystaniem analizy regresji

Analiza regresji prostej
Rozwiązywanie problemów z wykorzystaniem analizy regresji to proces, który powinien funkcjonować w każdym przedsiębiorstwie produkcyjnym czy usługowym na przynajmniej takim poziomie, aby przedsiębiorstwo w przypadku problemów mogło sprostać wymaganiom Klienta z punktu widzenia wydajności i jakości dostarczanych wyrobów.
Istnieje wiele metod i technik rozwiązywania problemów, z których najczęściej stosowaną jest połączenie diagramu Ishikawy (stawianie i selekcja hipotez) z metodą 5 WHY („weryfikacja” hipotez). Wykorzystanie tego zestawienia może sprawdzać się tylko w przypadku problemów prostych, niezłożonych technicznie.
W przypadku problemów złożonych, wieloczynnikowych, występujących w procesach generujących dużo danych numerycznych połączenie diagramu Ishikawy powinno odbywać się z narzędziami analizy statystycznej, tj. parametryczne i nieparametryczne testy statystyczne, analiza wariancji i kowariancji czy analiza korelacji i regresji (liniowej, nieliniowej, wielorakiej).
W niniejszym artykule przedstawiono przykład analizy regresji, mającej na celu potwierdzenie wpływu zmiennej X na zmienną Y oraz regulację predyktora (X) z na podstawie zakresu tolerancji zmiennej objaśnianej (Y).
Teoria dotycząca szacowania współczynników regresji.
Analiza regresji to metoda aproksymacji zależności cech zależnością funkcyjną oraz oceną dokładności tej aproksymacji. W przypadku, gdy dwuwymiarowy rozkład badanych cech jest zgodny z rozkładem normalnym, wtedy funkcja regresji przyjmuje postać liniową.
W praktyce, parametry liniowej funkcji regresji zastępuje się ich estymatorami, których wartości wyznacza się za pomocą metody najmniejszych kwadratów:
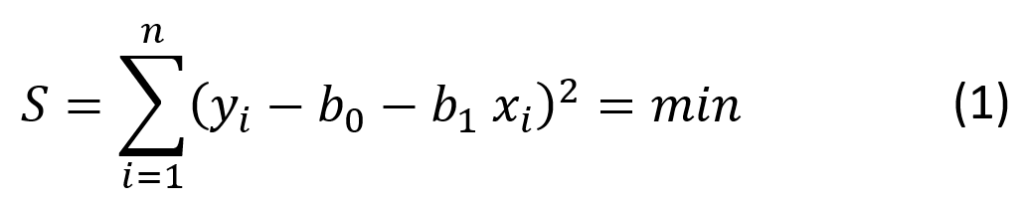
Gdzie: xi oraz yi to wartości obydwóch zmiennych dla kolejnej próby losowej.
Metoda najmniejszych kwadratów polega na takim wyznaczeniu wartości estymatorów b1 i b0, aby suma S osiągnęła minimum. Estymując współczynniki regresji b1 (współczynnik kierunkowy) oraz b0 (rzędna początkowa) otrzymuje się równanie:

gdzie:
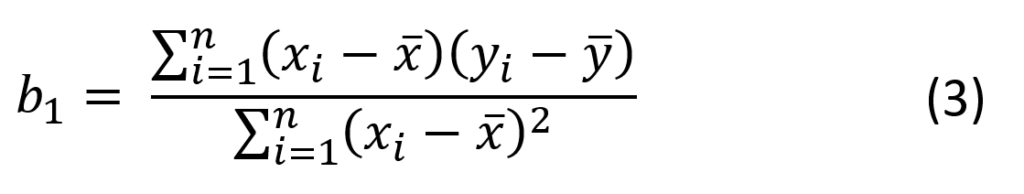
oraz:

Szacowanie współczynników regresji jest kluczowym etapem analizy zależności pomiędzy zmiennymi losowymi. W programie MS Excel można to zrobić na kilka sposobów. Poniżej przedstawiono 4 sposoby estymacji współczynników regresji.
Do obliczeń wykorzystano dane z regulacji procesu dokręcania łącznika gwintowego, gdzie zmienna X (twardość nakrętki stalowej) w sposób istotny wpływała na zmienną Y (moment formowania gwintu w technologii Taptite).
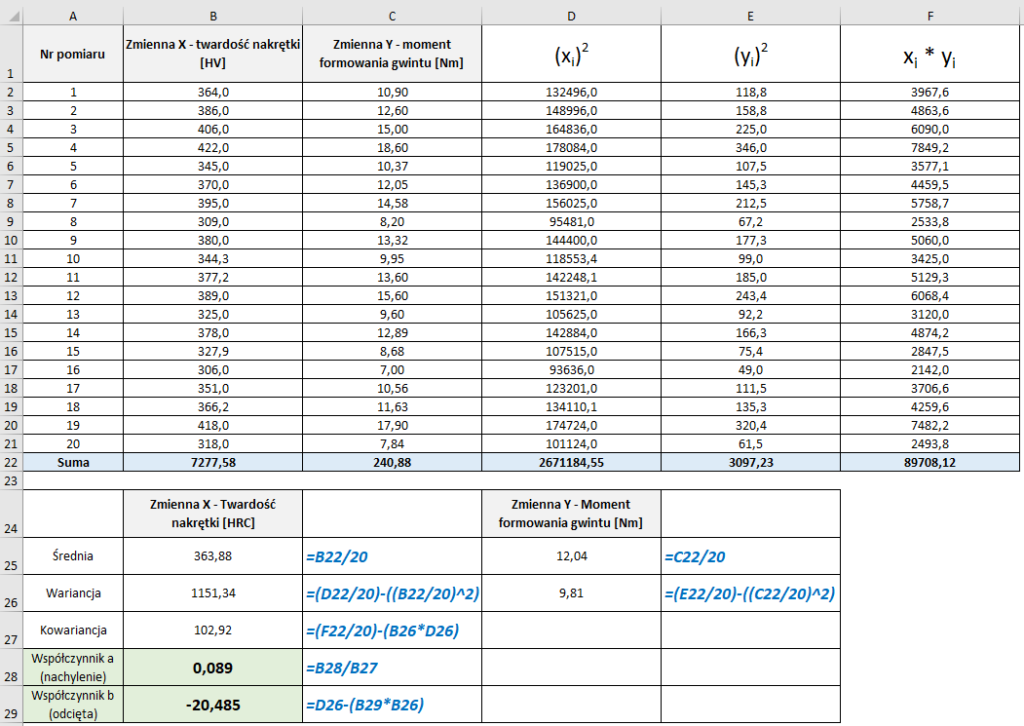
Sposób 1 – „na piechotę”, obliczania regresji zgodnie ze wzorami 2, 3, 4.
Na Rys. 1 przedstawiono sposób obliczeń współczynników regresji. Oszacowane współczynniki policzono w komórkach B28 oraz B29.
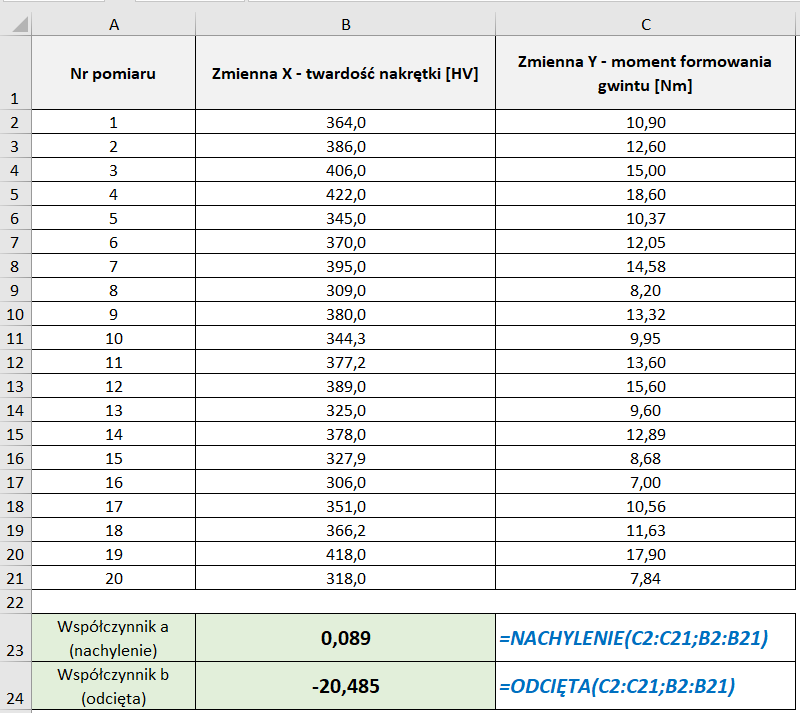
Sposób 2 – wykorzystanie formuł programu MS Excel.
Sposób 3 – obliczenia z wykorzystaniem dodatku Analysis ToolPak.
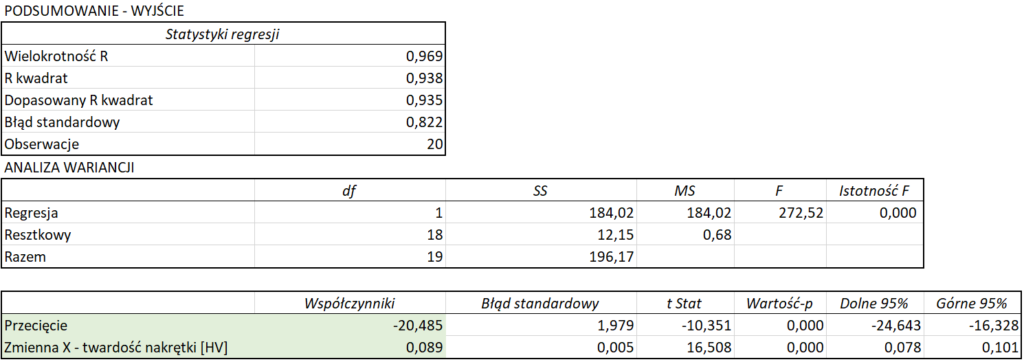
Wykorzystując ścieżkę Dane – Analiza Danych – Regresja uruchomiona zostanie zautomatyzowana procedura analizy regresji. Wprowadzając zakres wejściowy dla danych oraz wskazując komórkę, do której zrzucony zostanie wynik analizy, otrzymuje się wynik jak przedstawiono na Rys. 3.
Sposób 4 – obliczenie współczynników regresji z wykorzystaniem wykresu punktowego.
Wykorzystując ścieżkę Wstawianie – Wykres punktowy należy wstawić wykres, zaznaczając wcześniej zakres komórek z danymi zmiennych X i Y. Do wykresu należy dodać linię trendu liniowego idąc ścieżką Projekt wykresu – Dodaj element wykresu – Linia trendu – Liniowa. Następnie klikając na linię trendu uruchomić należy okno Formatowanie linii trendu i w Opcjach linii trendu włączyć Wyświetl równanie na wykresie.
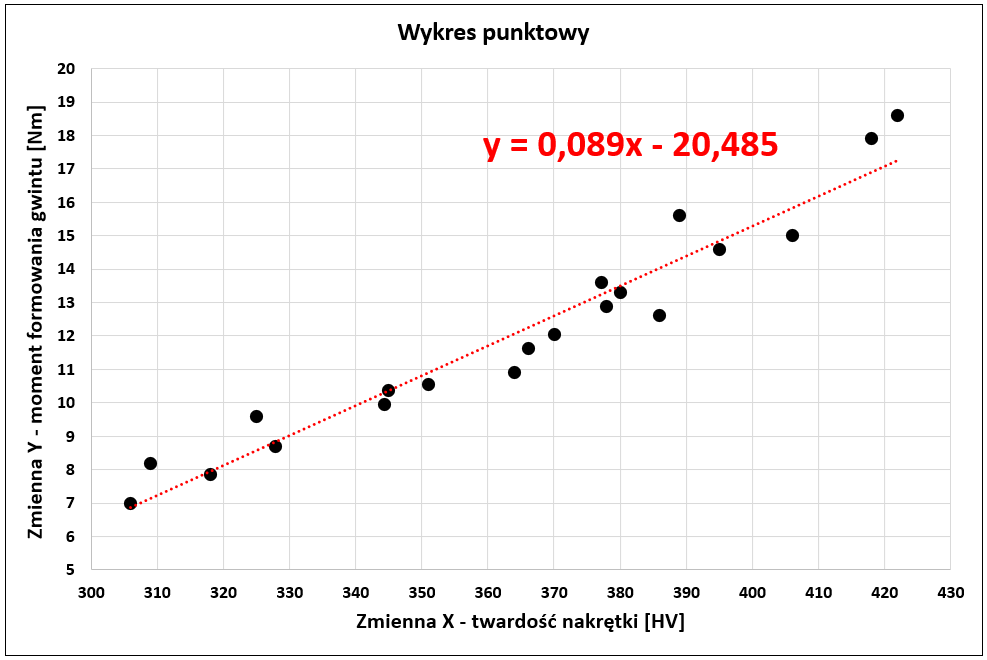
Dodatnia wartość współczynnika nachylenia (0,089) oraz kierunek nachylenia linii regresji wskazuje na korelację dodatnią, co oznacza, że wraz ze wzrostem twardości nakrętki stalowej (zmienna X) zwiększa się wartość momentu formownia gwintu (zmienna Y).
Mając do dyspozycji równanie regresji prostej oraz wykorzystując graficzne narzędzie Równoległobok Tolerancji wyznaczyć można zakres tolerancji dla zmiennej X, bazując na zakresie tolerancji zmiennej Y.
Na Rys. 5 przedstawiono sposób wyznaczania zakresu tolerancji dla twardości nakrętki stalowej.
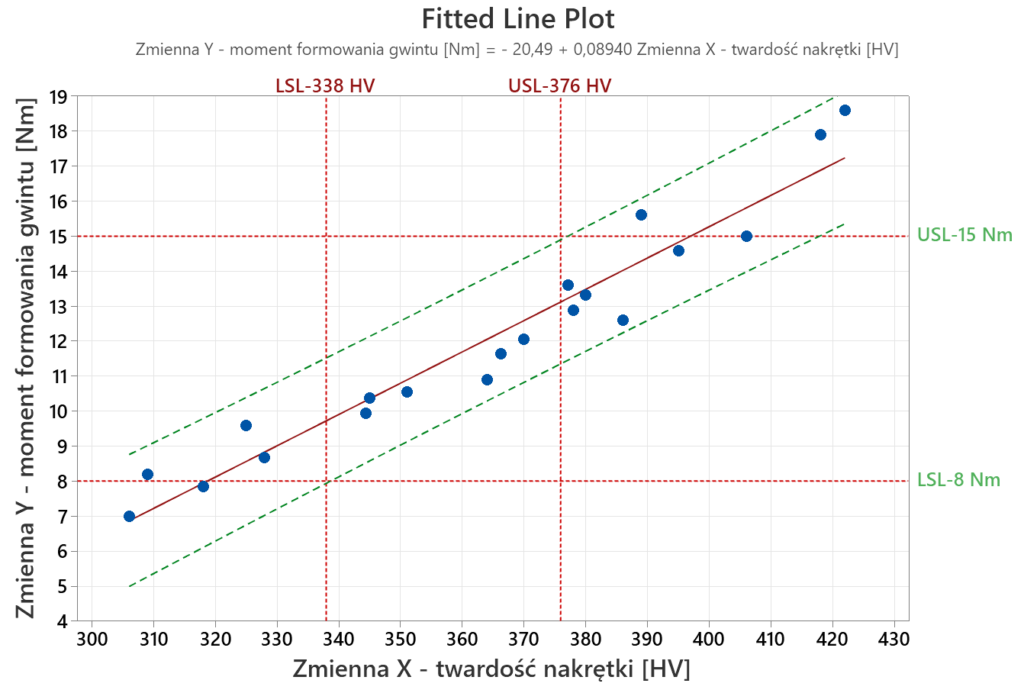
Z wykresu odczytać można, że jeżeli zakres tolerancji zmiennej Y zawiera się pomiędzy 8 – 15 Nm, to zakres tolerancji zmiennej X powinien zawierać się pomiędzy wartościami 338 – 376 HV.
Wniosek
Jeżeli producent nakrętek (dostawca) posiada możliwość technologiczną produkowania nakrętek w oszacowanym zakresie tolerancji twardości [HV], to montowania komponentów (klient) utrzymywał będzie wartość momentu formowania gwintu [Nm] w przyjętym zakresie tolerancji.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to udostępnij go w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
