Pp i Ppk dla danych „normalnych” i „nienormalnych”

Niniejszy artykuł ma na celu przybliżenie sposobu szacowania (estymacji) wskaźników wydajności procesu Pp i Ppk dla danych pochodzących z populacji o rozkładzie normalnym oraz z populacji o rozkładzie o prawostronnej asymetrii.
W mojej pracy zawodowej zbyt często spotykam się z sytuacją, w której analitycy danego przedsiębiorstwa dokonują szacowania wskaźników zdolności i wydajności procesu wykorzystując jeden, często pobrany z sieci plik obliczeniowy (MS Excel), który wykorzystywany jest do szacowania wartości wskaźników bez względu na charakter rozkładu danych.
Takie podejście prowadzi do obliczenia błędnych wartości wskaźników procesu.
W artykule tym omówione zostaną główne różnice w sposobie szacowania wskaźników Pp i Ppk z uwzględnieniem charakteru rozkładu danych empirycznych.
Wskaźniki Pp i Ppk dla rozkładu normalnego przedstawiono jako wskaźniki zmienności globalnej / całkowitej (ang. overall), w których zmienność liczona jest z wykorzystaniem estymatora odchylenia standardowego.
Pp i Ppk – teoria
Klasyczne wskaźniki wydajności procesu Pp i Ppk dla danych pochodzących z populacji o rozkładzie normalnym liczone powinny być zgodnie z poniższymi wzorami:

Gdzie:
s – to estymator odchylenia standardowego liczony wg wzoru:

Wskaźniki wydajności procesu Pp i Ppk dla danych pochodzących z populacji o istotnej asymetrii liczone powinny być zgodnie z poniższymi wzorami:
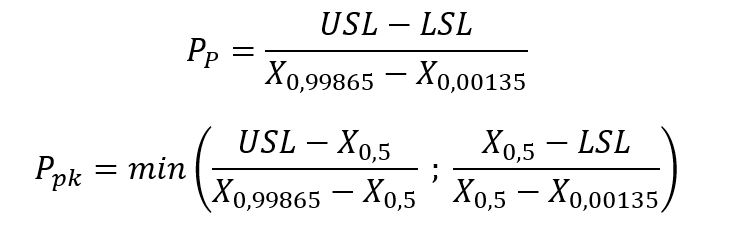
Gdzie:
- 50 percentyl zbioru to X0,5, czyli mediana.
- 99,865 percentyl zbioru to X0,99865.
- 0,135 percentyl zbioru to X0,00135.
Z czego wynika różnica mianowników wzorów?
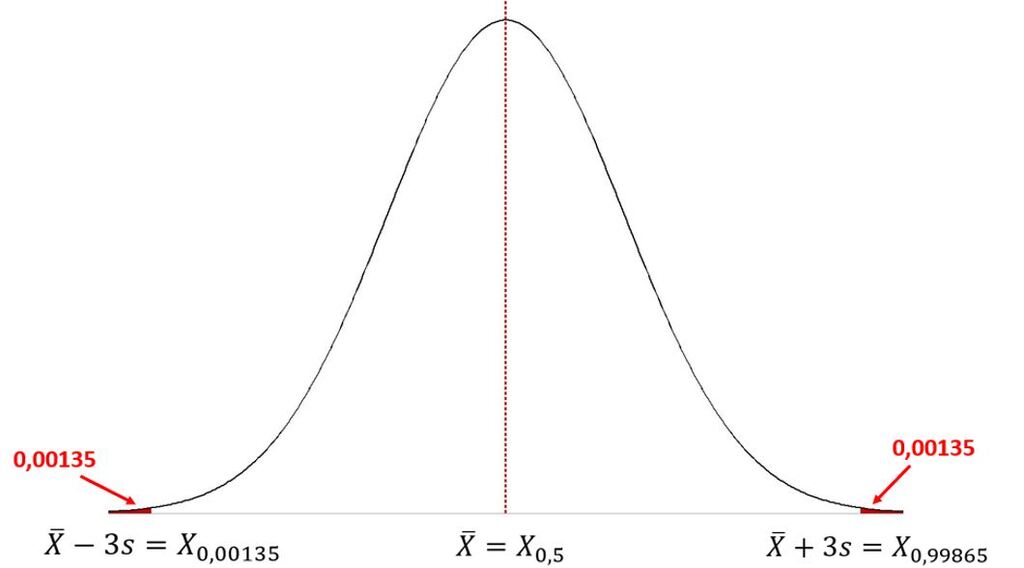
W idealnym (teoretycznym) i symetrycznym rozkładzie normalnym różnica wartości średniej arytmetycznej i mediany jest równa zero.
Wartość percentyla 99,865 policzyć można, dodając do wartości średniej arytmetycznej wartość trzech odchyleń standardowych.
Analogicznie, wartość percentyla 0,135 policzyć można, odejmując od wartości średniej arytmetycznej wartość trzech odchyleń standardowych.
Zależności przedstawiono na Rys.1.
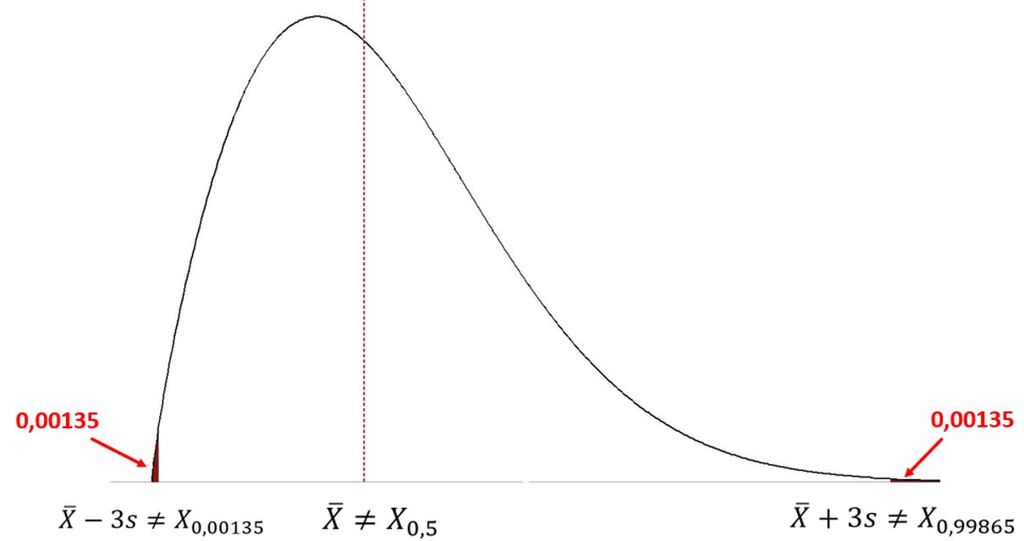
W rozkładzie o istotniej asymetrii zależność taka nie występuje:
- Wartości średniej arytmetycznej i mediany są różne.
- Wartość percentyla 99,865 jest wartością różną od wartości policzonej jako średnia arytmetyczna plus trzy odchylenia standardowe.
- Wartość percentyla 0,135 jest wartością różną od wartości policzonej jako średnia arytmetyczna minus trzy odchylenia standardowe.
Brak zależności przedstawiono na Rys.2.
Z powodu braku zależności przedstawionej na Rys.2 liczenie wartości wskaźników Pp i Ppk dla rozkładów asymetrycznych wykorzystując klasyczny wzór (z odchyleniem standardowym w mianowniku), daje błędne wartości tych wskaźników, a co za tym idzie zafałszowany obraz jakości procesu.
Sposoby policzenia wartości wskaźników Pp i Ppk w zależności od charakteru rozkładu danych przedstawiono w dwóch poniższych przykładach.
Przykład 1 – rozkład normalny
W tym przykładzie wartości percentylów 99,865 i 0,135 wyznaczone zostaną poprzez dodanie i odjęcie od wartości średniej wartości trzech odchyleń standardowych. Rozkład danych na tle zakresu pola tolerancji przedstawiono na Rys.3.
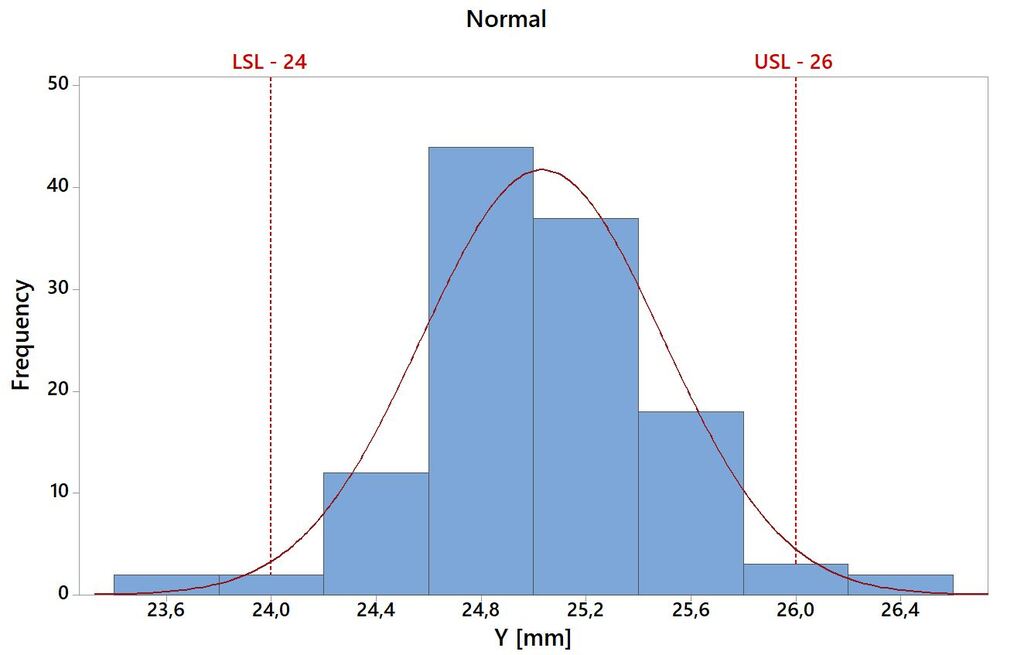
Dane:
- Średnia arytmetyczna – 25,03 [mm].
- Odchylenie standardowe – 0,46 [mm].
- USL – 26 [mm].
- LSL – 24 [mm].
Obliczenia:
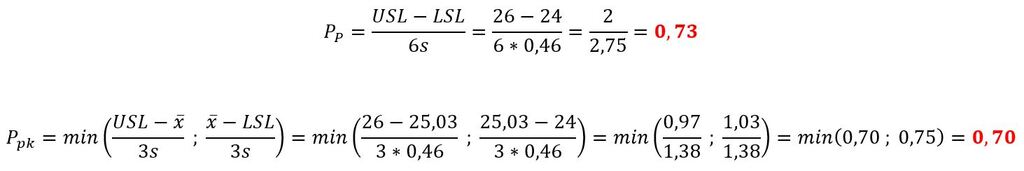
Przykład 2 – rozkład asymetryczny
W tym przykładzie z powodu istotnej asymetrii rozkładu danych, wartości percentylów 99,865 i 0,135 nie mogą zostać wyznaczone poprzez dodanie i odjęcie od wartości średniej wartości trzech odchyleń standardowych. Rozkład danych na tle zakresu pola tolerancji przedstawiono na Rys.4.
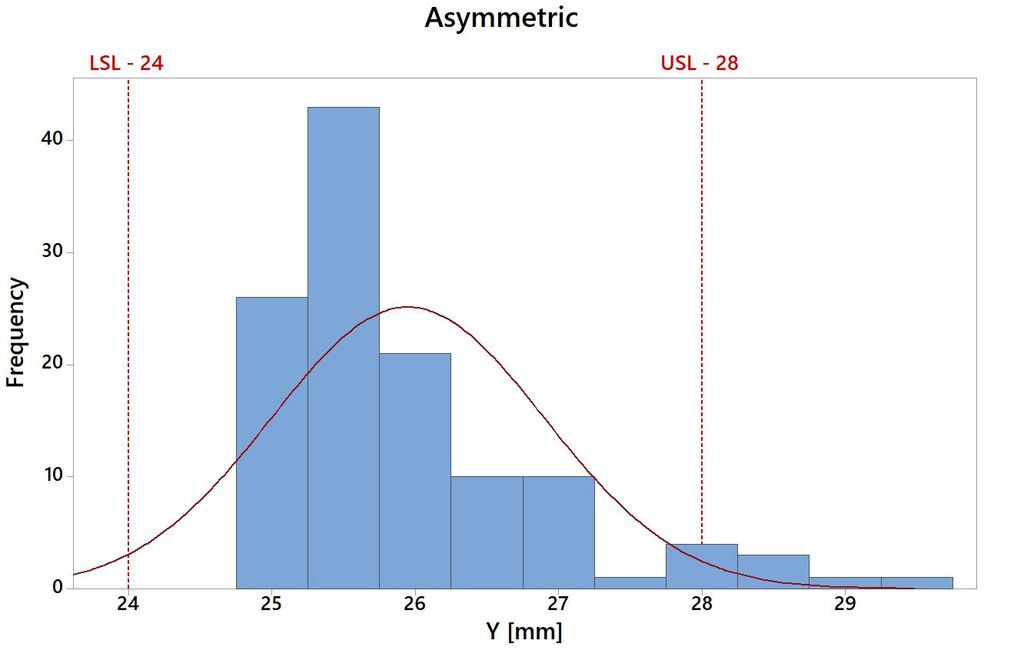
Pytanie: w jaki sposób policzyć wartości percentylów 99,865, 50 i 0,135?
Istnieje kilka metod wyznaczenia wartości tych percentyli, jedną z nich jest wykorzystanie wykresu dystrybuanty danego rozkładu teoretycznego.
Teoretyczną i empiryczną dystrybuantę CDF (ang. Cumulative Distribution Function) dla rozkładu asymetrycznego przedstawiono na Rys.5.
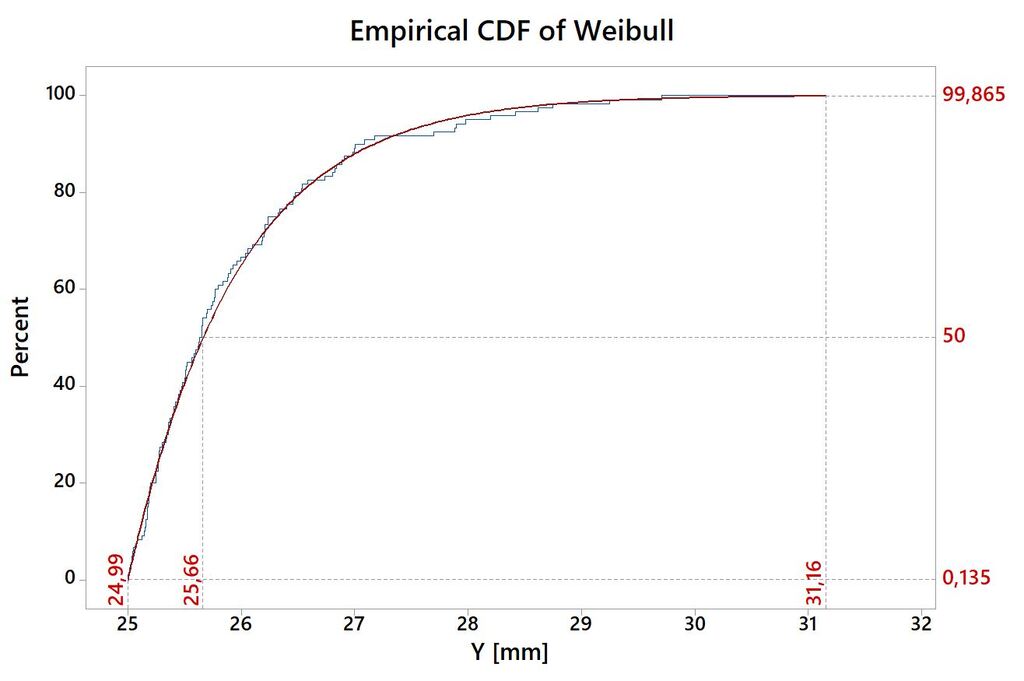
Z Rys.5. odczytać można, że wartość percentyla:
- 99,865 wynosi 31,16 [mm].
- 50 wynosi 25,66 [mm].
- 0,135 wynosi 24,99 [mm].
W związku z tym obliczenia dla pola toleranci USL = 28 i LSL = 24 przedstawiają się następująco:
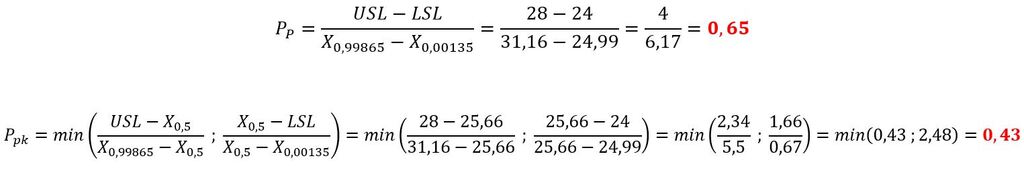
Pp i Ppk – podsumowanie
Podchodząc do analizy procesu z wykorzystaniem wskaźników wydajności Pp i Ppk obligatoryjne jest wykonanie analizy rozkładu danych.
Wykonanie takich testów jak:
- Normalności rozkładu danych.
- Identyfikacji obserwacji odstających.
- Stabilności procesu np. z wykorzystaniem kart kontrolnych Shewharta.
pozwoli na zwiększenie dokładności estymacji tych statystyk.
Należy zwrócić także uwagę na fakt, że wskaźniki zdolności i wydajności procesu będą tym dokładniej oszacowane, im stabilność procesu będzie lepsza – dla danych z procesów zawierających zmienną specjalną, wartości estymowanych wskaźników będą mniej dokładne.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Powiązane szkolenia:
.
.
.
.
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
