Metoda ANOVA w praktyce

Kontynuując poprzedni artykuł: (Test Bartletta w praktyce) zaznaczyć należy, że przed wykonaniem analizy wydajności procesu (obliczenie wskaźników Pp, Ppk), oprócz wykonania testu dla jednorodności wariancji w celu porównania rozrzutu danych, wykonać należy również analizę mającą na celu sprawdzenie, czy wartości przeciętne (średnie arytmetyczne) nie różnią się istotnie od siebie.
W tym celu wykonać można test weryfikujący jednorodność wielu średnich, czyli jednoczynnikową analizę wariancji (ANOVA).
Metoda ANOVA stosowana jest w celu weryfikacji czy przynajmniej trzy (lub więcej) średnie arytmetyczne pochodzą z jednej populacji.
Używając terminologii statystycznej, zakłada się hipotezę zerową (H0), która stanowi, iż średnie ze wszystkich prób (populacji) nie różnią się statystycznie od siebie, wobec hipotezy alternatywnej (H1), która stanowi, że przynajmniej jedna średnia różni się istotnie od pozostałych średnich.
Metoda ANOVA posiada niestety, kilka „słabości” – aby móc ją zastosować powinny zostać spełnione następujące założenia:
- Normalność rozkładu danych – analizowane próby, pochodzą z populacji o rozkładzie Gaussa.
- Jednorodność wariancji – próby nie różnią się istotnie od siebie pod względem wariancji (rozproszenia danych)
- Losowość (randomizacja) – próby są niezależne a sposób ich pobrania (wykonanie pomiarów) powinien być losowy i reprezentatywny.
W przypadku nie spełnienia jednego z powyższych warunków, wybiera się tzw. zamienniki testu ANOVA.
Na przykład, jeżeli nie zostanie spełniony warunek o jednorodności wariancji, zastosować można test ANOVA z tzw. poprawką Welcha.
Analizując dane z poprzedniego artykułu:
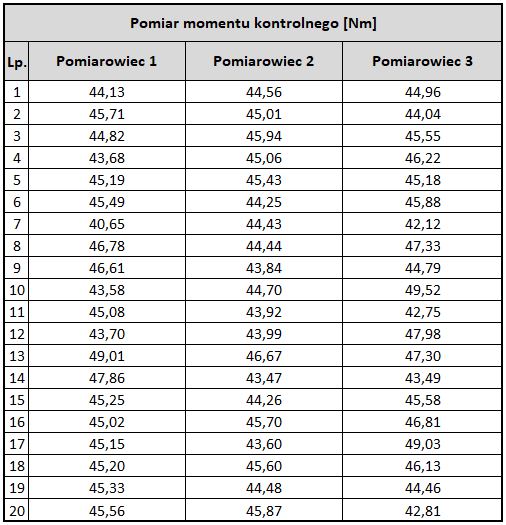
Wykorzystując statystykę testu Welcha:

można porównać wartości średnie arytmetyczne z pomiarów.
„Standardowy” test ANOVA nie powinien zostać zastosowany, ponieważ założenie o jednorodności wariancji nie zostało spełnione. Wynikiem testu Bartletta (p-value 0,0023) odrzucono hipotezę zerową, stanowiącą o jednorodności wariancji, natomiast przyjęto H1: przynajmniej jedna próba (pomiary jednego Kontrolera) różnią się istotnie od pozostałych pod względem rozproszenia danych.
W związku z tym, wykonano test Welcha, który zastosowanie ma w sytuacji, w której wariancje w próbach są nierówne.
Z wykorzystaniem testu Welcha obliczono wartość p-value, która wyniosła 0,207 (plik MS Excel z testem można pobrać tu).
Na tej podstawie nie odrzucono hipotezy zerowej i przyjęto, iż wartości średnie arytmetyczne z prób nie różnią się istotnie od siebie. Wnioskowano, że Pomiarowcy wykonują pomiary podobnie pod względem odtwarzalności pomiarowej.
W tym miejscu pojawiają się pytania:
- Jaki jest dalszy tok postępowania, jeżeli wartość p-value (obliczona w ramach testu ANOVA lub Welcha) byłaby mniejsza od przyjętego poziomu istotności statystycznej (np. 0,05) i hipoteza zerowa zostałaby odrzucona na korzyść alternatywnej stanowiącej, że przynajmniej jedna średnia różni się istotnie od pozostałych?
- Która lub które średnie różnią się istotnie pomiędzy sobą?
W takiej sytuacji należy kontynuować obliczenia wykonując procedury testów wielokrotnych, tzw. testy post-hoc, które stanowią dodatkowe testy dla testu ANOVA lub Welcha.
Testy post-hoc opiszemy w kolejnym artykule.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
