ISOPLOT – analiza systemu pomiarowego

ISOPLOT
to technika analizy systemu pomiarowego wywodząca się z procesu rozwiązywania problemów metodą Red X Shainina.
Analiza systemu pomiarowego
to kluczowa część procesu rozwiązywania problemów poprzedzająca czynności związane z poszukiwaniem przyczyny źródłowej.
Opisana metoda dotyczy systemów pomiarowych dla pomiarów powtarzalnych (nieniszczących).
Poprawny system pomiarowy powinien charakteryzować się odpowiednią, optymalną rozdzielczością (musi „widzieć” różnice pomiędzy mierzonymi częściami) oraz powtarzalnością pomiarową.
Odtwarzalność w tym przykładzie nie jest badana, ponieważ założeniem projektu rozwiązującego problem w metodzie Red X Shainina jest to, że pomiary zmiennej Y (analizowanej charakterystyki) w ramach projektu wykonywane są przez jedną osobę będącą członkiem zespołu rozwiązującego dany problem.
ISOPLOT
to proste narzędzie graficzne, które wykonane może być bez użycia jakiegokolwiek programu analizy statystycznej – wystarczy kartka papieru, linijka i ołówek. Oczywiście optymalnym środowiskiem do zbudowania ISOPLOT jest MS Excel i właśnie z użyciem tego programu przygotowano niniejszy artykuł.
ISOPLOT budowany jest wg następującego schematu:
- Przygotowanie narzędzia pomiarowego dla pomiarów nieniszczących (np.: suwmiarka, mikrometr, średnicówka, głębokościomierz, maszyna współrzędnościowa itp.). Narzędzie powinno być sprawne, kalibrowane na odpowiednich wzorcach, zgodnie z dedykowanymi normami i procedurami.
- Przygotowanie 30 sztuk elementów pomiarowych. Najczęściej są to części pobrane z procesu produkcyjnego. Wymiary części (analizowana charakterystyka) powinny pokrywać zakres zmienności procesu oraz być w zakresie pomiarowym narzędzia.
- Czytelne oznaczenie wszystkich 30 sztuk mierzonych elementów. Najwygodniej użyć cyfr arabskich: 1,2,3…30.
ISOPLOT – Wykorzystanie MS Excel:
- Do arkusza MS Excel np. do komórek A2:A31 wprowadzić oznaczenia części, które podlegać będą pomiarom.
- Wykonać pierwszą serię pomiarową wszystkich 30 elementów w kolejności losowej. Osoba wykonująca pomiary nie powinna wiedzieć, którą część mierzy (nie powinna znać nr części).
- Wyniki należy zapisać w arkuszu MS Excel w zakresie komórek B2:B31.
- Wykonać drugą serię pomiarową, utrzymując zasady takie jak w serii pierwszej.
- Wyniki zapisać w zakresie komórek C2:C31. Ważne: pomiary z obydwóch serii muszą być sparowane.
- Do komórek A1, B1, C1 wprowadzić oznaczenia, nagłówki tak jak przedstawiono na Rys. 1.
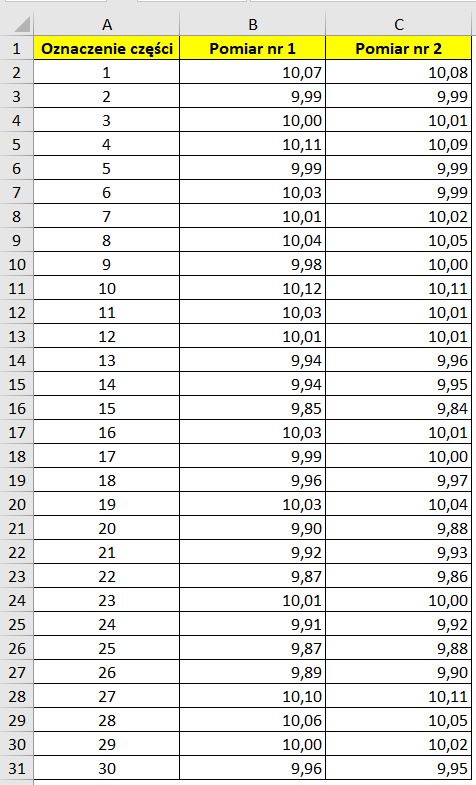
Dane z dwóch serii pomiarowych przedstawić używając wykresu punktowego w taki sposób, iż na osi X znajdują się pomiary pierwszej serii a na osi Y drugiej serii pomiarowej (Rys.2). Wyskalować osie X i Y, tak aby wartości minimalne i maksymalne osi były takie same.
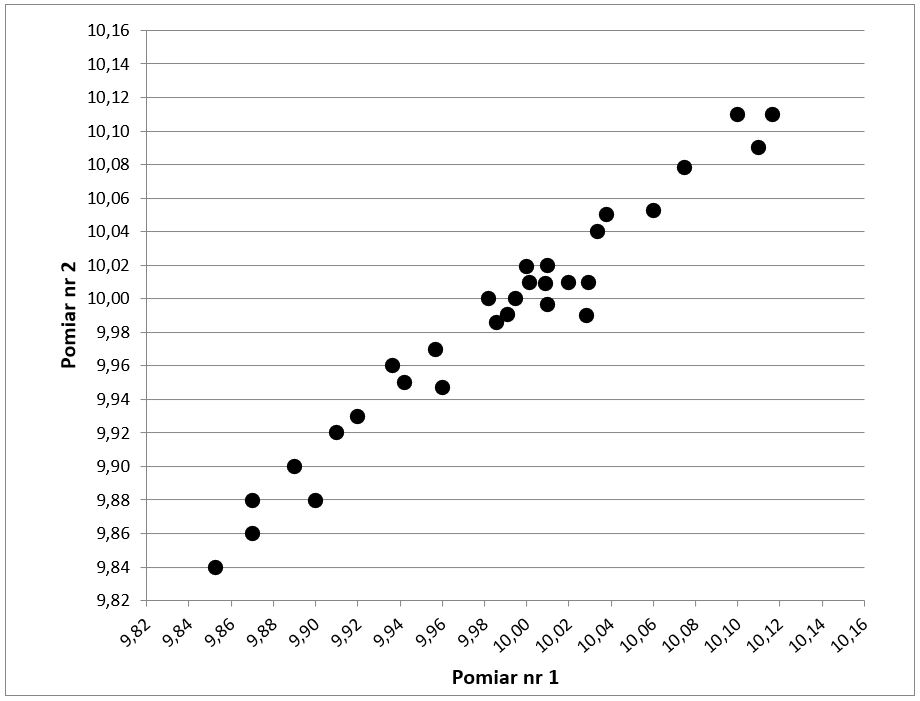
Dodać linię trendu liniowego (Rys.3).
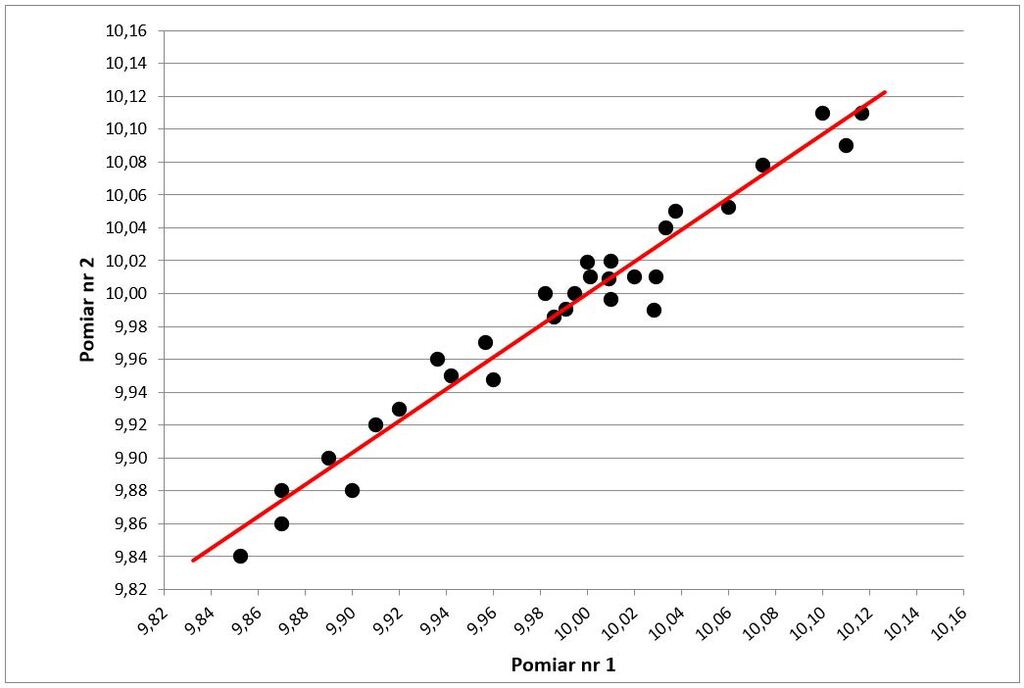
Pomijając punkt najbardziej oddalony od linii trendu, wyznaczyć górną i dolną linię limitu, tworząc w ten sposób przedział ufności (predykcji) dla pomiarów. Pierwszą linię limitu (w tym przypadku dolną) wyznaczyć tak, aby przechodziła przez drugi najdalszy punkt od linii trendu i przebiegała równolegle do linii trendu. Drugą linię limitu wyznaczyć tak, aby znajdowała się w takiej samej odległości od linii trendu co linia pierwsza i również przebiegała równolegle do linii trendu (Rys.4).
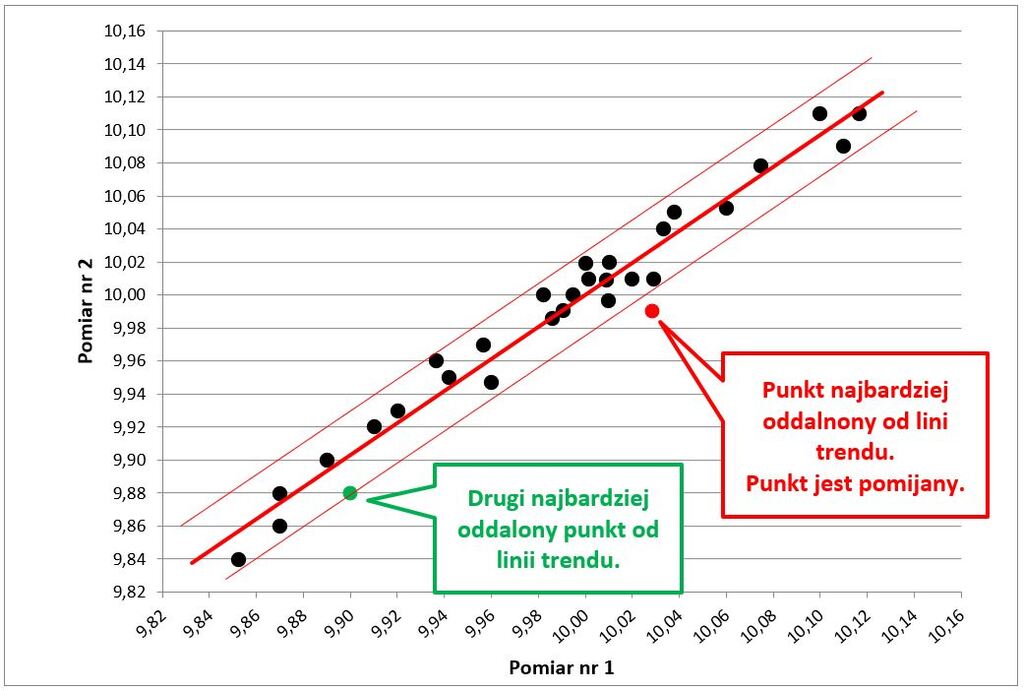
Na końcach linii wyznaczyć dwa okręgi, których środek znajdował się będzie dokładnie na linii trendu, a obwód przebiegać będzie przez najbardziej skrajny punkt pomiarowy. Okręgi wpasowane będą w linie limitu (Rys.5).
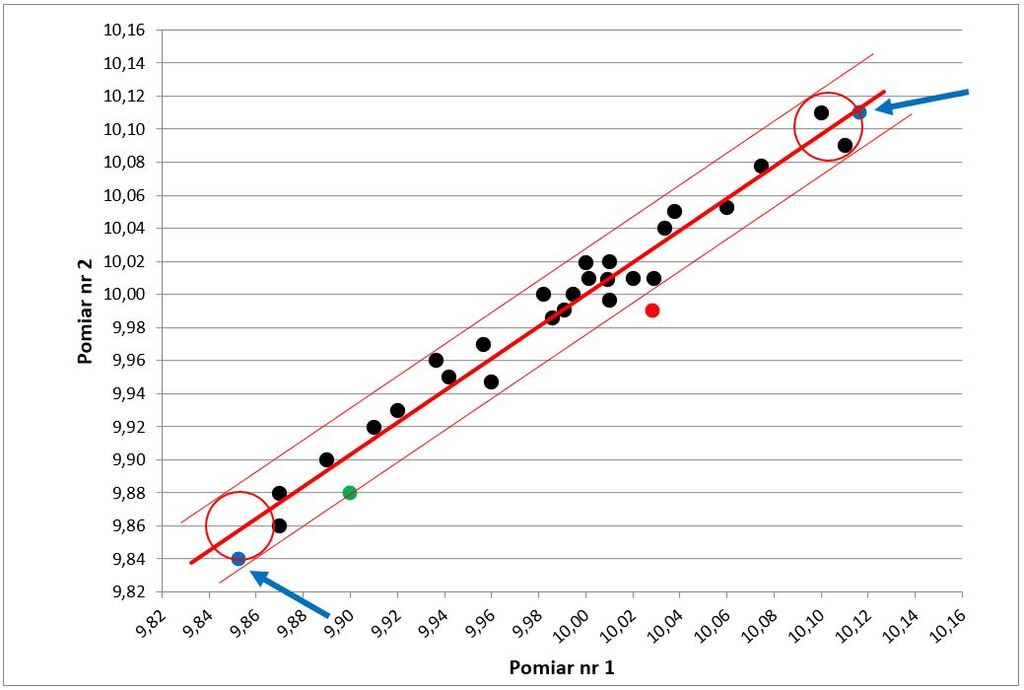
Z punktów styku linii okręgu z linią trendu poprowadzić dwie proste prostopadłe do osi X (Rys.6). Odczytać wartości na osi X w miejscu styku z prostymi. Policzyć różnicę pomiędzy wartościami. Różnicę traktować jako liczbową wartość rozrzutu (zmienności) procesu (PV).

Dokonać pomiaru odległości pomiędzy liniami limitu (Rys.7). Zmierzoną wartość traktować jako liczbową wartość rozrzutu (zmienności) systemu pomiarowego (MV).

Obliczyć Współczynnik Decyzji wskazujący czy system pomiarowy jest odpowiedni pod względem powtarzalności do użycia w procesie rozwiązywania problemu. Współczynnik obliczyć wg wzoru:
WD1 = PV / MV
Jeżeli zajdzie zależność: WD1 > 6 to można uznać, iż przyrząd pomiarowy jest wystarczająco dobry do przeprowadzenia analizy pod względem powtarzalności pomiarowej.
W powyższym przykładzie:
PV = 10,12 – 9,84 = 0,28
MV = 10,03 – 10,00 = 0,03
WD1 = 0,28 / 0,03 = 9,3
Ponieważ zaszła relacja: WD1 9,3 > 6 system pomiarowy uznaje się za zgodny ze względu na powtarzalność.
Obliczyć Współczynnik Decyzji wskazujący czy system pomiarowy jest odpowiedni pod względem rozdzielczości. Współczynnik obliczyć wg wzoru:
WD2 = PV / rozdzielczość urządzenia pomiarowego
Jeżeli zajdzie zależność: WD2 > 10 to można uznać, iż przyrząd pomiarowy jest wystarczająco dobry do przeprowadzenia analizy pod względem rozdzielczości (w języku metody Red X mówi się „że system pomiarowy jest w stanie odróżnić część BOB od części WOW”).
W powyższym przykładzie:
WD2 = 0,28 / 0,01 = 28
Ponieważ zaszła relacja: WD2 28 > 10 system pomiarowy uznaje się za zgodny ze względu na rozdzielczość.
ISOPLOT – podsumowanie
Przedstawiony w artykule ISOPLOT jest metodą niezwykle prostą, niewymagającą skomplikowanych obliczeń. Narzędzie to powstało w czasie, w którym nie było ogólnie dostępnych programów komputerowych (nie istniał jeszcze program MS Excel) i w całości prowadzona była z użyciem kartki, ołówka i linijki.
Z tego powodu wykorzystana może być przez osoby nie mające umiejętności analitycznych i pracowników bezpośrednio produkcyjnych do szybkiej oceny systemu pomiarowego.
Metoda Red X Shainina na tle innych metod rozwiązywania problemów wyróżnia się mnogością narzędzi i technik statystycznych, lecz są to techniki niezwykle proste i łatwe do zrozumienia i użycia.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
