Inżynier procesu montażu połączeń gwintowych

Inżynier procesu montażu połączeń gwintowych związany jest z szeroką znajomością procesu łączenia elementów za pomocą łączników gwintowych (śrub, wkrętów, nakrętek).
.
Wiedza, jaką inżynier powinien dysponować, zaczyna się od znajomości zagadnień z zakresu:
- Inżynierii materiałowej.
- Trybologii i tarcia.
- Geometrycznych właściwości elementów konstrukcyjnych złącza gwintowego.
- Metod statystycznej analizy danych.
Inżynier począwszy od tak trywialnej umiejętności, jaką jest identyfikacja na podstawie znaków na łbie śruby klasy wytrzymałościowej, poprzez umiejętność obliczenia optymalnego momentu dokręcania, statystycznego porównania pomiarów momentu kontrolnego kilku osób wykonujących pomiary, do wykonania eksperymentu opartego na wieloczynnikowej analizie wariancji w ramach DoE (planowanych eksperymentów).
Montaż połączeń gwintowych w przedsiębiorstwie podzielić można na 3 główne etapy:
- Dokręcanie łączników gwintowych.
- Kontrola jakości dokręconych łączników gwintowych.
- Proces rozwiązywania problemów występujących podczas dokręcania i kontroli łączników gwintowych.
1. Proces dokręcania łączników gwintowych.
W zależności od technologicznych rozwiązań procesu dokręcania (zastosowanie ręcznych, pneumatycznych lub elektrycznych narzędzi dynamometrycznych) Inżynier powinien potrafić mapować i optymalizować operacje dokręcania. Na przykład, zastosowanie odpowiedniej kombinacji narzędzi pneumatycznych i ręcznych narzędzi dynamometrycznych typu 2, pozwala na prawie całkowitą eliminację zjawiska relaksacji z połączenia gwintowego. Zjawisko relaksacji objawia się spadkiem siły osiowej w łączniku gwintowym powstałej wskutek redukcji naprężeń elementów będących jego częścią. Redukcja ta powstawać może w wyniku dopasowania się powierzchni elementów dokręcanych, drgań, czy odkształcania plastycznego elementów złącza gwintowego podczas dokręcania (np. uszczelki stalowe czy miedziane).
W przypadku zastosowania droższych, o wiele bardziej precyzyjnych narzędzi elektrycznych sterowanych elektronicznie, zjawisko relaksacji eliminowane może być poprzez zastosowanie wielokrokowej strategii dokręcania. Dysponując takimi narzędziami, możliwe jest także ustawienie zabezpieczeń (Poka-Yoke / error proofing), których celem jest kontrola jakości dokręcania. Wykorzystanie pełnych możliwości narzędzi jest niezbędne, szczególnie w produkcji masowej, w której liczba dokręceń danego rodzaju łącznika osiąga nawet kilkaset w ciągu jednej zmiany produkcyjnej.
Optymalizacja procesu dokręcania polega w pierwszej kolejności na doborze odpowiednich narzędzi montażowych, a następnie pełne wykorzystanie ich możliwości technologicznych.
Jeżeli przedsiębiorstwo dokonało inwestycji w drogie (nawet kilkadziesiąt tysięcy złotych za sztukę) elektryczne narzędzia dokręcające, to ich wykorzystanie powinno być optymalne. Oznacza to, że narzędzie nie powinno pracować tylko jako wkrętarka, ale jako pełnowartościowy i zaawansowany system dokręcająco–kontrolny.
Na przykład dokręcanie realizowane w strategii na określony moment dokręcania, powinno zawierać elementy kontroli zmiennej losowej, jaką jest kąt dokręcania. Na Rys.1 przedstawiono podstawowy schemat możliwości zabezpieczenia kąta obrotu w dwukrokowej strategii dokręcania na określony moment.
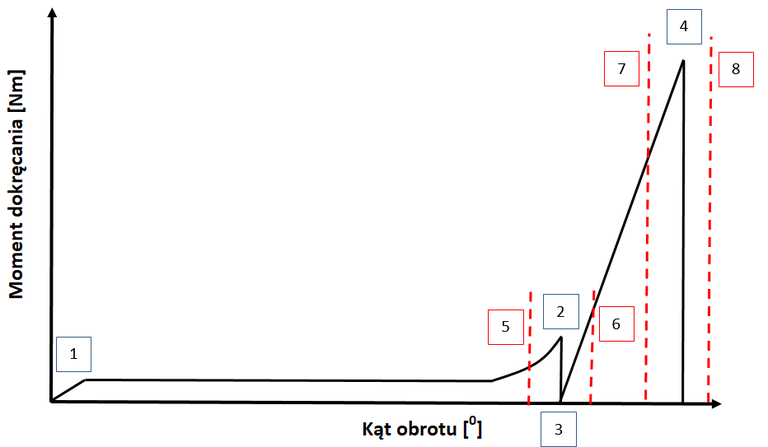
Wytłumaczenie rys.1.
Pierwszy krok dokręcania rozpoczyna się w punkcie (1). Jest to chwila, w której wkrętarka elektryczna jest włączana a śruba rozpoczyna się obracać luźno. To tzw. krok „rundown”. Koniec pierwszego kroku następuje w punkcie (2), który jest wyznacząną eksperymentalnie wartością momentu dokręcania.
W chwili (2) dochodzi do styku łba śruby z elementem łączonym. Zabezpieczenie tego punktu statystycznie obliczonymi granicami kątowymi (5) i (6) jest kluczowe ze względu na jakość montażu. Można w ten sposób kontrolować np.: dobór odpowiedniej długości śruby lub jakość gwintu zewnętrznego i wewnętrznego. Krótko mówiąc: dokręcanie musi osiągnąć zadaną wartość momentu (2) i jednocześnie osiągnięcie tej wartości musi znaleźć się w zakresie kątowym zdefiniowanym granicami (5) i (6). Tylko wtedy, gdy będzie spełniony ten warunek pierwszy krok dokręcania uznany zostanie za zgodny.
Analogicznie wygląda sytuacja dla kroku drugiego (dokręcanie finalne na zadany moment dokręcania) rozpoczynającego się w punkcie (3) i kończącego w (4). Osiągniecie finalnego momentu dokręcania, powinno zawierać się w statystycznie obliczonych granicach (7) i (8), których celem jest np. niedopuszczenie do sytuacji „płynięcia” połączenia wskutek niepożądanego plastycznego odkształcania się elementów połączenia gwintowego.
Powyższy przykład dotyczy dwukrokowej strategii dokręcania, jednak liczba kroków może być większa, powodując że prawidłowe dokręcenie będzie musiało spełnić większą liczbę warunków jakości dokręcenia.
O ilości kroków decyduje charakter połączenia gwintowego oraz wiedza i doświadczenie pracownika dokonującego optymalizacji. Kluczowe jest to, aby przed obliczeniem granic dla kąta, dokonać optymalizacji procesu dokręcania mającej na celu minimalizację zmienności rozkładu kąta obrotu. Jedną z polecanych metod statystycznych w tym celu jest przeprowadzanie eksperymentu z wykorzystaniem ortogonalnych planów metody Taguchi.
Problemem podczas obliczania granic kontrolnych dla kąta obrotu okazać się może fakt, że jego rozkład w większości przypadków nie jest zgodny z rozkładem normalnym. Dlatego użycie klasycznych wzorów wykorzystujących estymator odchylenia standardowego w mianowniku wprowadzi istotny błąd estymacji, którego efektem będzie wyłączanie się narzędzia dokręcającego podczas dokręcania (sygnał NOK) w sytuacji, w której dokręcanie przebiega zgodnie.
2. Proces kontroli dokręconych łączników gwintowych.
Proces kontroli dokręconych łączników gwintowych dotyczy w głównej mierze aktywności z zakresu metod MSA (analiza systemu pomiarowego) oraz SPC (statystyczne sterowanie procesem).
MSA dotyczy w pierwszej kolejności przeprowadzenia badania ręcznego narzędzia dynamometrycznego wskazującego typu 1, zgodnie z wytycznymi zawartymi w normie PN-EN ISO 6789-1,2:2017, która w roku 2018 ostatecznie zastąpiła wersję poprzednią z 2009.
Następnym krokiem jest przeprowadzenie analizy systemu pomiarowego, czyli narzędzia i człowieka wykonującego pomiar. Ponieważ pomiar momentu dokręconej śruby jest pomiarem niepowtarzalnym, wykorzystanie klasycznej metody ARM (metoda wartości średniej i rozstępu) lub ANOVA krzyżowa jest nieodpowiednie.
Do przeprowadzenia tej analizy wykorzystuje się metodę ANOVA zagnieżdżona, która dedykowana jest dla pomiarów niepowtarzalnych.
Przed przystąpieniem do działań z zakresu SPC, należy potwierdzić statystycznie, że wszystkie osoby wykonujące pomiary (ang. Appraisers) na danym stanowisku pomiarowym, wykonują je nieistotnie różnie ze względu na powtarzalność i odtwarzalność pomiarową. W tym celu posłużyć się można narzędziami z zakresu statystyki matematycznej.
Działania SPC skupiają się w pierwszym kroku na statystycznym obliczeniu zakresu pola tolerancji dla momentu kontrolnego, a następnie kontrolowania i sterowania procesem kontroli momentów.
Do sterowania procesem kontroli momentów łączników gwintowych wykorzystuje się narzędzia statystyczne takie jak:
- Narzędzia główne: karty kontrolne Xbar-R/S, Xi-MR.
- Narzędzia pomocnicze: test Grubbsa dla wartości odstających, testy dla wartości średniej czy dla wariancji, które stosowane są w przypadku produkcji wielostrumieniowej (np. kilka śrub w jednej operacji montażu: 5 śrub mocujących koło samochodu osobowego).
Poniżej przedstawiono przykład analizy kontroli momentów dokręconego łącznika dla procesu jedno strumieniowego (jedna śruba łącząca elementy). Na Rys. 2. przedstawiono dane w formie wykresu liniowego, które analizowane są tylko na podstawie zakresu pola tolerancji. Taki sposób prowadzenia kontroli jest niewystarczający i należy uzupełnić go o analizę w stosunku do statystycznie obliczonych linii krytycznych (kontrolnych) UCL i LCL.
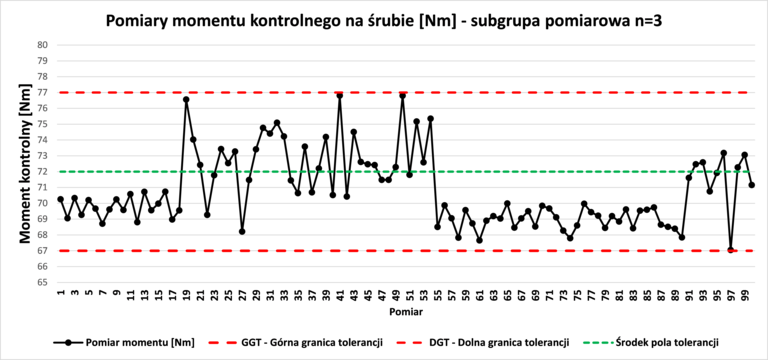
Z wykresu odczytać można tylko, że pomiary (do tej pory) znajdują się w zakresie pola tolerancji. Wprawny analityk dostrzeże jednak, że występuje czasowe przesunięcie rozkładu momentów kontroli oraz zmiana jego rozrzutu. Natomiast, brakuje na to statystycznego dowodu. Taki dowód można uzyskać, wykorzystując jedną z kart kontrolnych. Na Rys. 3. zaprezentowano kartę kontrolną wartości średniej, zbudowaną na podstawie 3-elementowej podgrupy.

Z karty odczytać można, że niektóre wartości średnie oznaczone jako (1), znajdują się poza statystycznie wyznaczonymi liniami krytycznymi. Oznacza to, że proces nie znajduje się pod statystyczną kontrolną i powinien zostać wyregulowany.
Co więcej, średnie oznaczone jako (2), to kolejne wartości 9 i 10 znajdujące się po jednej stronie linii wyznaczonej przez wartość średnią z pomiarów (linii centralnej). Wskazuje to na czasowe (istotne statystycznie) przesunięcie procesu w stronę wartości wyższych.
Analogicznie wygląda sytuacja dotycząca średnich oznaczonych (2) znajdujących się poniżej linii centralnej. Widoczne jest także przesunięcie średniej procesu poniżej środka pola tolerancji o około 1,2 Nm.
Dewiacja dotyczy także zmienności w podgrupach co pokazano na Rys.4., na którym przedstawiono kartę odchylenia standardowego.
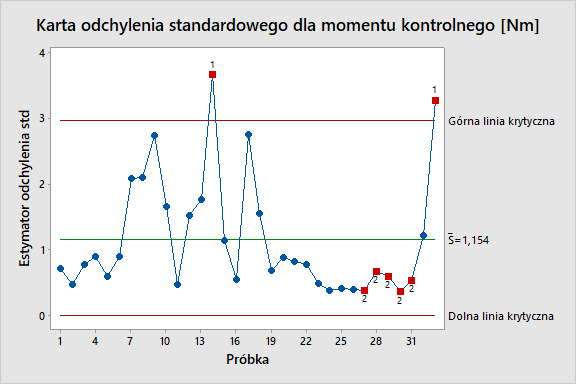
Na rys.4 zauważyć można, że dwie próbki oznaczone (1), znajdują się ponad górną linią krytyczną. Oznacza to, że zmienność w obrębie tych próbek była istotnie większa niż w pozostałych.
Ponadto próbki oznaczone (2), to 9, 10, 11, 12 i 13 kolejna próbka, znajdująca się poniżej linii wartości średniej liczonej z estymatorów odchyleń standardowych wszystkich podgrup (zielona linia). Oznacza to, że istnieje kilka próbek (znajdujące się poniżej zielonej linii), w których zmienność jest istotnie niższa niż w pozostałych. Należy szukać przyczyny tej pozytywnej sytuacji i doprowadzić, aby w przyszłości wartości estymatorów odchylenia standardowego dla wszystkich podgrup zbliżone były do tych oznaczonych jako (2).
Dalsza analiza dotyczy obliczenia wskaźników zdolności i wydajności procesu, przedstawiono na Rys.5.

Wartości wskaźników Cpk i Ppk są niższe od krytycznej wartości 1,33. Wartości wskaźników Cp i Pp są istotnie różne od siebie (ich przedziały ufności nie pokrywają się wzajemnie). Różny kształt krzywych dzwonowych (nie pokrywają się) wskazuje również, że w procesie występuje tzw. zmienna specjalna, powodująca czasowe przesunięcie procesu. Kształt histogramu jest niesymetryczny, co w tym przypadku potwierdza dryf pomiarów w zakresie pola tolerancji. Z powodu braku stabilności procesu wartości wskaźników powinny traktowane być z rezerwą, ponieważ ich estymacja nie jest dokładna.
Przedstawiony proces nie znajduje się w stanie statystycznego uregulowania i powinien zostać poddany analizie mającej na celu znalezienie przyczyny źródłowej tego stanu.
3. Proces rozwiązywania problemów występujących podczas dokręcania i kontroli łączników gwintowych.
Proces rozwiązywania problemów występujących podczas dokręcania i kontroli łączników gwintowych, wykorzystauje się w celu poprawy jakości oraz przywrócenia stanu statystycznego uregulowania procesu.
Rozwiązywanie problemów realizowane jest z użyciem nie tylko podstawowych technik i metod takich jak: diagram-przyczynowo skutkowy (diagram Ichikawy), 5 razy dlaczego (ang. 5 WHY), metoda 5W2H czy burza mózgów, ale także na podstawie bardziej zaawansowanych technik Doriana Shainina (Red X) czy z wykorzystaniem narzędzi metody Six Sigma.
Jednym z najczęściej spotykanych problemów w procesie montażu połączeń gwintowych jest zjawisko odkształcenia plastycznego śruby lub gwintu wewnętrznego w otworze, które prowadzi do obniżenia wytrzymałości złącza, a nawet do zerwania śruby. Powodem powstawania tego zjawiska może być nieprawidłowo w stosunku do cech geometrycznych oraz właściwości mechanicznych i trybologicznych, obliczona wartości momentu dokręcania.
Bardzo dobrym narzędziem wnioskowania statystycznego używanym w tym przypadku jest wieloczynnikowa analiza wariancji prowadzona na podstawie przygotowanego wcześniej planu eksperymentu. Testowaniu poddać można takie czynniki (zmienne objaśniające X) jak między innymi: twardość śrub, nakrętek i podkładek, średnica podziałowa gwintu zewnętrznego i (lub) wewnętrznego, prędkość obrotowa dokręcania, ilość kroków dokręcania itp.
W praktyce czynników powodujących problem może być nawet kilkanaście, dlatego ważne jest, aby wyselekcjonować z nich 3-4, które odpowiadają przynajmniej za 70% zmienności zmiennej objaśnianej (Y).
Zmienną (Y) w tym przypadku może być punkt uplastycznienia połączenia gwintowego, pole powierzchni pod krzywą dokręcania czy nachylenie krzywej dokręcania w zakresie stosowalności prawa Hooke’a (w zakresie odkształceń sprężystych).
W celu wyselekcjonowania 2-4 czynników spośród kilkunastu stosuje się np. plany eliminacyjne Placketta-Burmana. W ich wyniku, przeprowadza się analizę opartą na planie pełno czynnikowym (ang. full factorial), w wyniku którego oprócz wpływu czynników głównych oszacować można także wpływ interakcji pomiędzy czynnikami.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Powiązane szkolenia:
.
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
