Minitab – wykresy Multi-Vari
Wykresy Multi-Vari są graficznym narzędziem przedstawiającym oraz organizującym dane w sposób ułatwiający identyfikację zmienności (wariancji) zmiennej objaśnianej Y. Wykresy te (budowane np. w programie Minitab) są często używane w sytuacjach, w których zmienność jest trudno dostrzegalna. Służą także do pokazania związków pomiędzy czynnikami (zmienne X) a odpowiedzią (zmienna Y).
Mogą być używane zarówno w stosunku do danych historycznych z procesu (np. z pomiarów charakterystyk w ramach kontroli jakości) jak również w stosunku do danych „przyszłych” np. analiza danych zbieranych w ramach przygotowanego pod konkretny problem arkusza kontrolnego.
Przed wykonaniem wykresów należy określić zmienną Y (analizowaną charakterystykę kontrolną), która wyrażona powinna być w skali interwałowej lub ilorazowej oraz wybrać czynniki (zmienne X) mogące wywierać wpływ na zmienną Y. W wytypowaniu czynników pomóc może analiza z wykorzystaniem diagramu Ichikawy. Zmienne X wyrażone mogą być zarówno w skali nominalnej czy porządkowej, jak również odpowiednio zakodowanych skalach interwałowej i ilorazowej.
Wykresy Multi-Vari stosowane są w sytuacji, w której analizowane są przynajmniej dwie zmienne X.
W najnowszej wersji (na dzień 27.11.2019) programu Minitab 19.2 wykonać można analizę nawet dla 8 czynników. Dodatkowo w tej wersji dodano możliwość wykonania wykresu odchyleń standardowych dla analizowanych poziomów czynników.
Przykład zastosowania analizy z wykorzystaniem wykresu Multi-Vari w programie Minitab.
Opis problemu:
W procesie dokręcania kół jezdnych do samochodu dostawczego stwierdzono problem polegający na tym, że na niektórych kołach maszyna dokręcająca kończyła operację dokręcania ze statusem NOK.
Opis rozwiązania problemu z użyciem programu Minitab:
Po wykonaniu analiz wstępnych (5W2H, diagram Ichikawy, 5WHY) Inżynier procesu pobrał dane z maszyny dokręcającej i wykonał analizę wydajności procesu dokręcania. Analizę wykonano dla rozkładu finalnego kąta dokręcania. Wynik analizy przedstawiono na Rys.1.
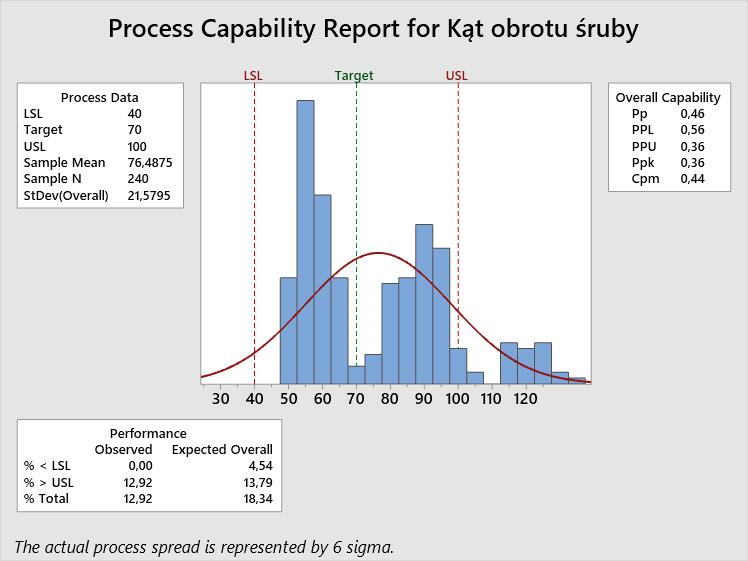
Z analizy wydajności wynika, iż istnieje problem z wielomodalnością rozkładu danych. Zamiast jednego histogramu o symetryczności zbliżonej do rozkładu normalnego, widoczne są trzy mniejsze histogramy wskazujące na czasowe (lub nie) przesunięcia rozkładów z pomiarów. Część pomiarów znajduje się poza górną granicą tolerancji dla finalnego kąta dokręcania.
Z dostępnych danych wynika, iż zmienność kąta dokręcania może być analizowana w oparciu o 4 następujące czynniki:
- X1 – dzień produkcji samochodów (3 poziomy: poniedziałek, wtorek, środa).
- X2 – zmiana produkcyjna, na której dokręcane są koła (2 poziomy: zmiana A i B).
- X3 – rodzaj dokręcanego koła (2 poziomy: koła stalowe i koła ze stopu aluminium).
- X4 – wrzeciono dokręcające (5 poziomów. Koło samochodu osobowego mocowane jest za pomocą 5 śrub, z których każda dokręcana jest przez niezależne wrzeciono / wkrętarkę elektryczną).
Na Rys. 2. przedstawiono wykres dla danych pobranych z maszyny dokręcającej, segmentowanych wg w/w wymienionych czynników. Plik MS Excel z danymi można pobrać tu: plik.

Wnioski:
- Z wykresu wynika, iż istnieje różnica pomiędzy poziomami czynnika X3 (rodzaj dokręcanego koła). Zauważyć należy, że rozkład kąta dokręcania dla kół stalowych lokuje się przeciętnie w okolicach 58 stopni obrotu, natomiast rozkład kąta dokręcania dla kół aluminiowych przeciętnie w okolicach 95 stopni obrotu.
- Widoczna jest także różnica w wartościach kąta dokręcania dla wrzeciona nr 3 (czynnik X4), ale tylko dla kół ze stopu aluminium, przeciętną wartość kąta można lokować w okolicy 120 stopni obrotu i można powiedzieć o interakcji pomiędzy czynnikami X3 i X4.
Działania zaradcze:
- Przygotowanie dwóch programów dokręcania oddzielnie dla kół stalowych i kół ze stopu aluminium.
- Przekazanie wkrętarki nr 3 do kalibracji i ewentualnej naprawy.
Podsumowanie:
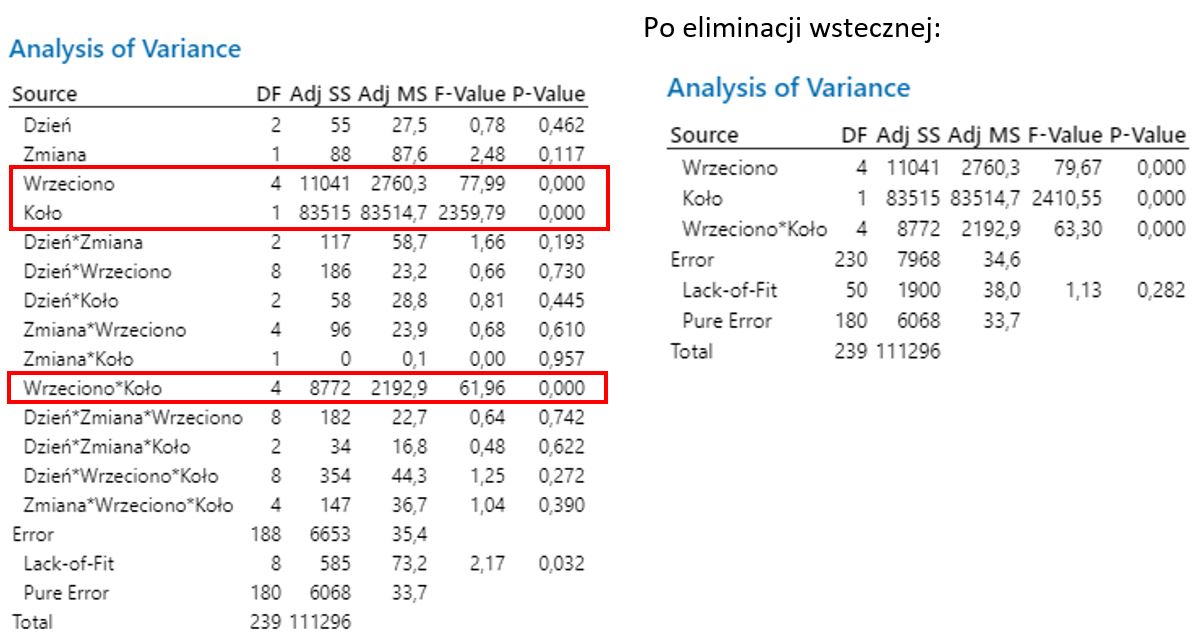
Wykresy Multi-Vari to narzędzia, które przy prawidłowym wykorzystaniu mogą stać się potężnym sprzymierzeńcem w rozwiązywaniu problemów związanych ze zmiennością specjalną w procesach produkcyjnych. Korzystając z programu Minitab przygotowanie takiego wykresu zajmuje niewiele czasu i nie jest czynnością skomplikowaną. Analizę z użyciem wykresów Multi-Vari można stosunkowo prosto uzupełnić o analizę wariancji z użyciem ogólnego modelu liniowego, co jest przedstawione na Rys.3.
Minitab – wykresy Multi-Vari aktualizacja: 14.04.2020
Aktualizacją (nr 19.2020.1) programu Minitab z dnia 7 Kwietnia 2020 roku powrócono do układu z wersji 18 programu (dla narzędzia Multi-Vari) i dodano narzędzie Variability Chart.
Narzędzie Multi-Vari Chart wykorzystać można do analizy zmienności zmiennej Y, wynikającej tylko ze średnich arytmetycznych poziomów czynnika i tylko do maksymalnie 4 czynników (zmienna X) w jednym badaniu.
Narzędzie Variability Chart służy do analizy zmienności zmiennej Y, wynikającej zarówno ze średnich arytmetycznych oraz estymatorów odchylenia standardowego poziomów czynnika, jak i dodatkowo aż do 8 czynników w jednym badaniu.
Miejsce uruchomienia tych narzędzi statystycznych pokazano na Rys. 4.

Przykład wykorzystania narzędzi
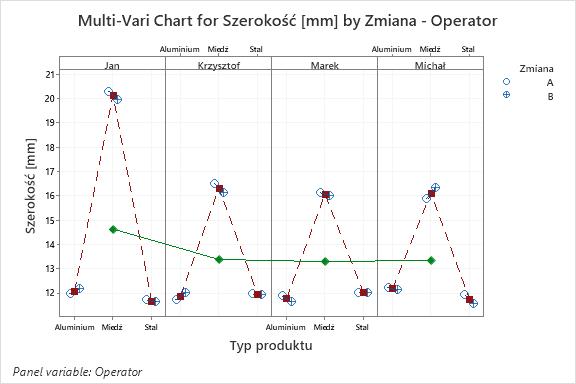
Załóżmy, że chcemy oszacować wpływ 3 czynników (X):
- Zmiana produkcyjna: A / B.
- Typ materiału: Aluminium / Miedź / Stal.
- Operator: Jan / Krzysztof / Marek / Michał.
Na zmienność zmiennej Y: szerokość szczeliny [mm].
Wykorzystując narzędzie Multi-Vari otrzymamy jeden wykres tylko dla średnich arytmetycznych:
.
Wykorzystując narzędzie Variability Chart otrzymamy dwa wykresy, gdzie pierwszy dla średnich arytmetycznych, drugi dla estymatorów odchylenia standardowego:
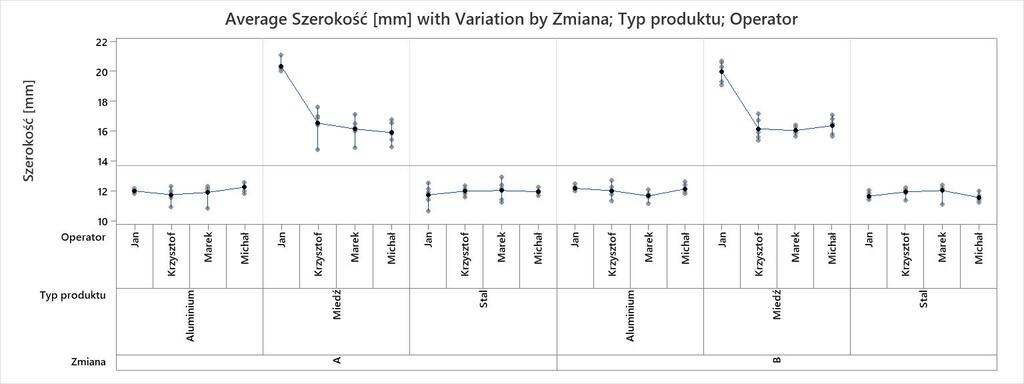
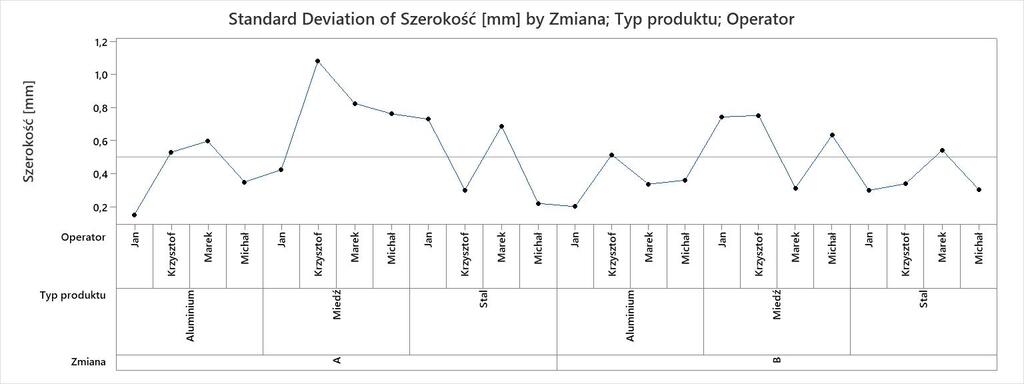
.
Przygotowania, wykonania i interpretacji wykresów Multi-Vari nauczyć się można uczestnicząc w naszym szkoleniu: Problem Solving – Skuteczne Rozwiązywanie Problemów
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
.
