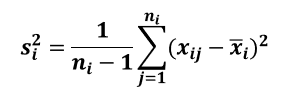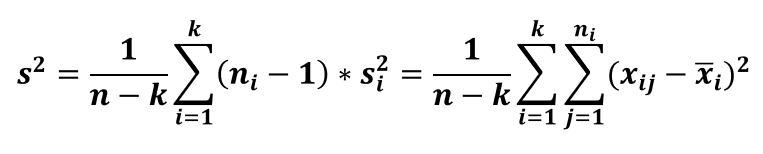Test Bartletta w praktyce
Wstęp
Test Bartletta, nazywany tak od nazwiska jego autora, wykorzystywany jest przede wszystkim jako test poprzedzający test jednorodności wielu średnich (jednoczynnikowa ANOVA), w którym zakłada się jednorodność wariancji w badanych populacjach. Innym zastosowaniem może być chęć porównania rozproszenia danych w przypadku procesów wielostrumieniowych (wielostanowych) przed wykonaniem analizy wydajności procesu (obliczanie wskaźników Pp i Ppk). Zostało to opisane w niniejszym artykule na przykładzie danych pochodzących z pomiarów momentu kontrolnego na dokręconym łączniku gwintowym. Pomiary wykonywane przez trzech różnych pomiarowców pracujących na różnych zmianach produkcyjnych (ranna, popołudniowa, nocna) na tym samym odcinku linii produkcyjnej i tym samym montażowym stanowisku pracy.
Test Bartletta – przebieg
Test Bartletta stosowany jest do porównania rozproszenia badanej cechy (wariancji) w przypadku, gdy rozważaniom poddaje się więcej niż dwie próby losowe. Zakłada się przy tym, że populacje, z których pobrano próby losowe posiadają rozkłady normalne N(mi, σi) (i=1,2,…, k).
Weryfikacji poddaje się hipotezę zerową o jednakowych wariancjach we wszystkich populacjach, czyli: 
, wobec hipotezy alternatywnej H1 formułowanej następująco: nie wszystkie wariancje są jednakowe. Na podstawie pomiarów (prób losowych) dokonuje się obliczeń:
- Nieobciążonych estymatorów wariancji we wszystkich populacjach:
- Łącznego oszacowania wariancji:
- Poprawki c:
gdzie n jest liczebnością całkowitą obliczaną wg wzoru:
- Obliczenia statystyki χ2 zgodnie ze wzorem:
która ma przy założeniu prawdziwości H0 rozkład χ2 o k-1 stopniach swobody. Obszar krytyczny w tym teście buduje się jako prawostronny. Do ustalenia wartości p-value wykorzystuje się rozkład χ2.
Test Bartletta w praktyce – studium przypadku
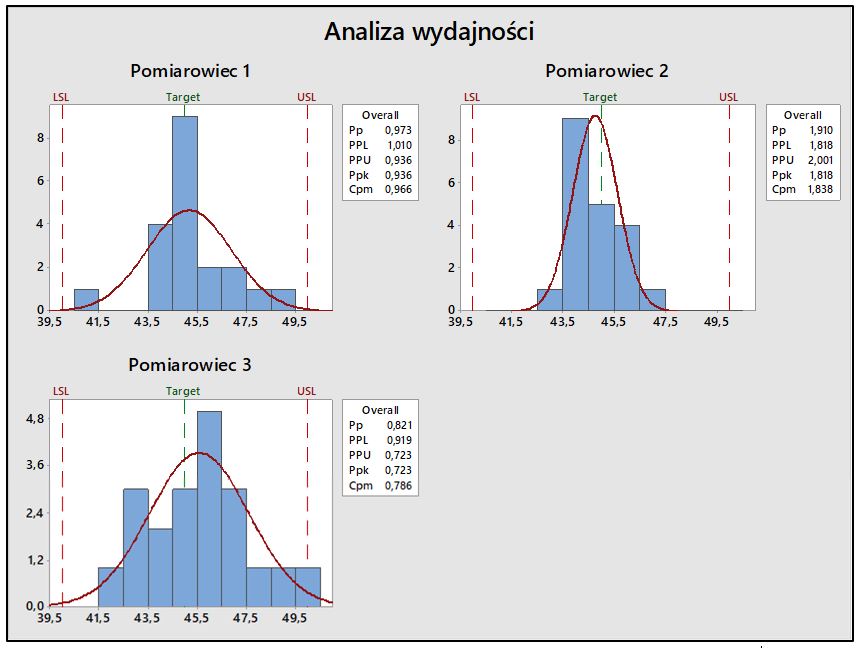
Analizie wydajności procesu poddano pomiary momentu kontrolnego wykonywane na dokręconych łącznikach gwintowych (śrubach). Pomiary wykonane zostały przez trzech Pomiarowców (jak opisano we wstępie) za pomocą ręcznego narzędzia dynamometrycznego typu 1 klasy C. Zakres pola tolerancji dla momentu kontrolnego zawierał się pomiędzy 40 Nm (DGT) a 50 Nm (GGT). Na Rys. 1 przedstawiono wartości momentów kontrolnych dla każdego Pomiarowca.
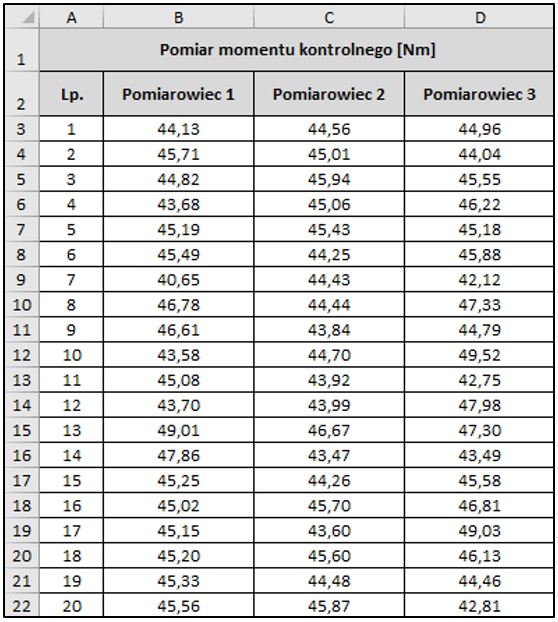
Gdyby błędnie rozpocząć analizę wydajności procesu analizując dane ze wszystkich trzech prób łącznie, otrzymano by następujące wyniki analizy:
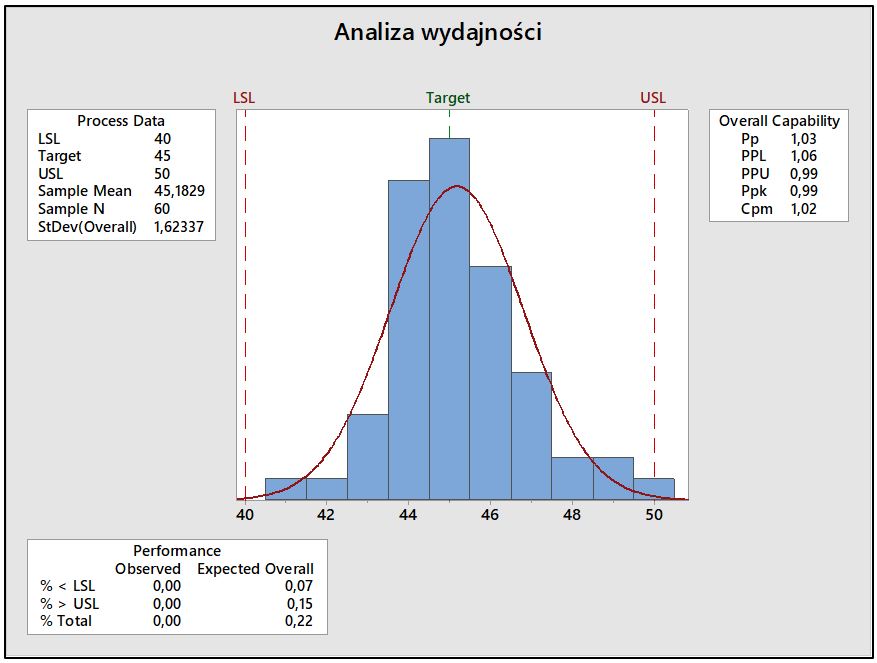
Obliczone wskaźniki Pp (1,03) i Ppk (0,99) nie spełniły przyjętego wymagania wynoszącego dla tych wskaźników w tym procesie minimalną wartość 1,33. Wskazano także na wynoszące 0,22% prawdopodobieństwo pojawienia się pomiarów poza granicami tolerancji. Mając na uwadze, że dane pochodzą z trzech strumieni (Pomiarowców), poddano je analizie ze względu na jednorodność wariancji z wykorzystaniem testu Bartletta. Sposób obliczeń prowadzonych w programie w MS Excel na podstawie opisanych wyżej wzorów przedstawiono na Rys.3.:
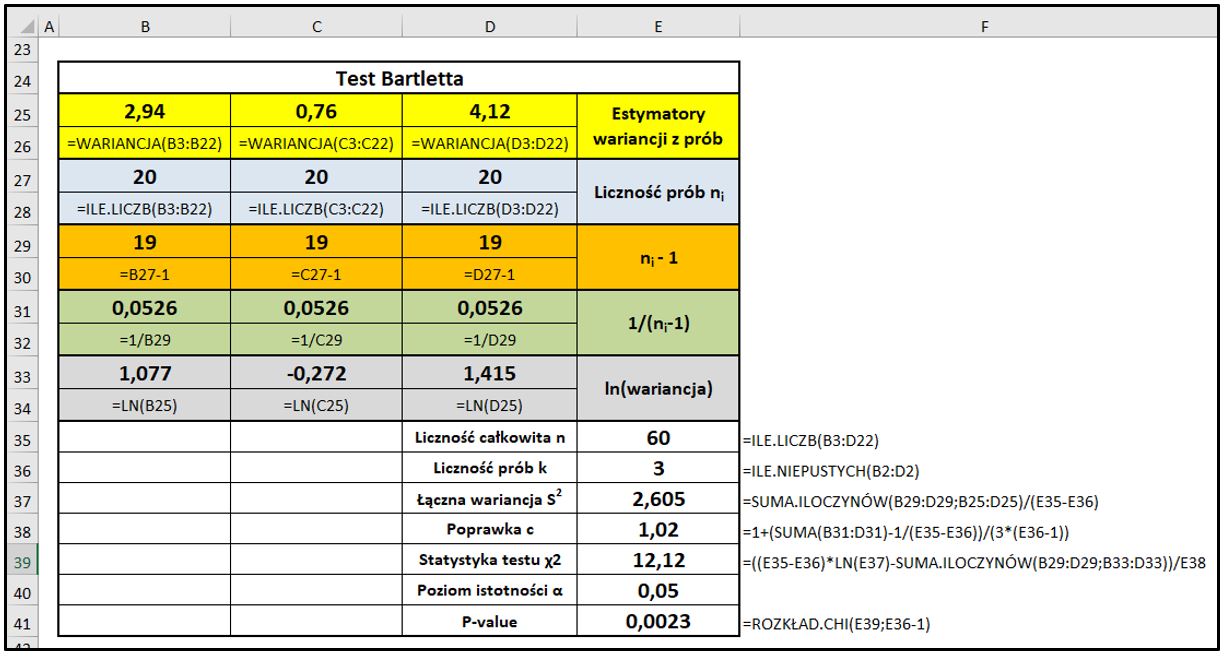
Obliczona wartość p-value (0,0023) okazała się mniejsza od przyjętego poziomu istotności statystycznej α0,05, co jednoznacznie wskazuje, że rozproszenie danych (wariancje) w analizowanych próbach (pomiarach) trzech Pomiarowców, są istotnie statystycznie różne. Zwracając uwagę na wartości estymatorów wariacji, wnioskować można, że Pomiarowiec nr 2 wykonuje pomiary najbardziej powtarzalnie. Na podstawie wyniku testu, podjęto następujące decyzje:
- Wykonania analizy wydajności procesu osobno dla każdego Pomiarowca, co przedstawiono na Rys. 4.
- Przeprowadzenie szkolenia i warsztatu praktycznego, którego celem było nauczenie Pomiarowców 1 i 3 wykonywania pomiarów momentu kontrolnego na śrubie tak, jak wykonuje to Pomiarowiec 2.
Podsumowanie
Wykorzystanie statystyki wnioskującej, w skład której wchodzą między innymi testy parametryczne w analizie zdolności i wydajności procesu jest niezbędne, w przypadku analizowania danych pochodzących z procesów wielostanowych, ale również jednostanowych. W procesach jednostanowych nie wykorzystuje się testów porównawczych, ale z pewnością dane pomiarowe należy poddać testom dla obserwacji odstających, losowości próby czy normalności rozkładu.
Można spotkać się ze stwierdzeniem: „Nie ma dobrego SPC bez odpowiedniego MSA”, jednak zdaniem autora stwierdzenie należy rozwinąć do: „Nie ma dobrego SPC bez odpowiedniego MSA i statystyki opisowej oraz wnioskującej”.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.