Nieparametryczny test Manna-Whitneya

Teoria dotycząca testu Manna-Whitneya
W niniejszym artykule omówiony został nieparametryczny test Manna-Whitneya w udoskonalonej wersji zaproponowanej przez Wilcoxona. Test ten używany jest do zweryfikowania hipotezy zakładającej, że dwie próby pochodzą z tej samej populacji lub też, że dwie populacje, z których pobrano próby, mają taki sam rozkład.
Test ten bardzo często stosowany jest jako alternatywa dla parametrycznego testu t-Studenta dla dwóch średnich, wtedy gdy niespełniony jest warunek o normalności rozkładu badanej zmiennej losowej.
W teście Manna-Whitneya nie ma warunku normalności rozkładu, wystarczy tylko, że wyniki pomiarów da się wyrazić w skali porządkowej, a także gdy zmienna losowa ma charakter skokowy.
W teście tym wykorzystuje się tzw. rangowanie, czyli przypisywanie kolejnym wartościom uporządkowanego ciągu obserwacji kolejnych liczb naturalnych wskazujących pozycję danej wartości w tym ciągu.
Przy dostateczne dużych (powyżej 10) liczebnościach obydwu prób suma rang R1 z dostateczną (z praktycznego punktu widzenia) dokładnością podlega rozkładowi normalnemu, przy czym parametry tego rozkładu można obliczyć wykorzystując wzory:

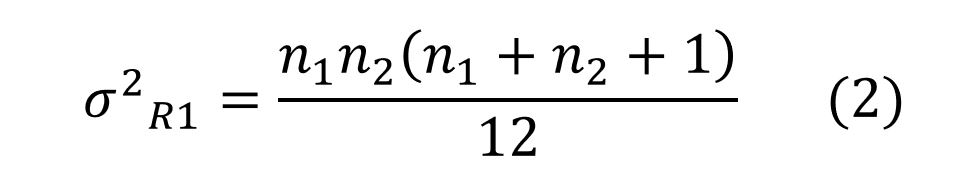
Weryfikację przeprowadza się po uprzedniej standaryzacji sumy rang R1 za pomocą wzoru:
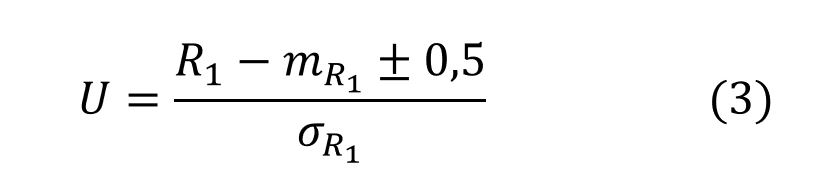
Statystyka U ma przy założeniu prawdziwości hipotezy zerowej rozkład N(0,1), zatem wnioskowanie odbywa się z wykorzystaniem tego rozkładu. Wartość 0,5 we wzorze dodaje się, gdy suma rang R1 < mR1, natomiast odejmuje w przypadku przeciwnym (R1 > mR1).
Powyższy opis byłby kompletny, gdyby nie problem rang wiązanych. Korekta, jaką należy uwzględnić, dotyczy wariancji sumy rang. Po uwzględnieniu wpływu rang wiązanych wzór (2) zostanie zastąpiony w obliczeniach następującym wzorem:

Gdzie:
g jest liczbą grup skupiających rangi wiązane,
tj jest liczbą wiązanych rang w j-tej grupie.
Przykłady problemów, które można rozwiązać z wykorzystaniem testu Manna-Whitneya
Przykład 1 (wartości cechy wyrażone są w skali porządkowej):
Z dwóch klas szkoły średniej wylosowano po 6 dzieci i otrzymano następujące wyniki badania inteligencji (tzw. iloraz inteligencji), klasa A: 110, 112, 115, 98, 130, 123, oraz klasa B: 88, 135, 140, 138, 95, 125. Na poziomie istotności α0,05 zweryfikować hipotezę, że obydwie próby pochodzą z jednej populacji dzieci o określonym rozkładzie ilorazu inteligencji.
Przykład 2 (zmienna losowa wyrażona w skali ilorazowej lecz ma charakter skokowy):
Kierownik sklepu z płytami kompaktowymi chce sprawdzić, czy dwóch sprzedawców ma taką samą liczbę sprzedanych płyt czy może jeden z nich sprzedaje więcej. Dane sprzedaży w ujęciu miesięcznym dla sprzedawcy A: 35, 44, 39, 50, 48, 29, 60, 75, 49, 66, oraz dla sprzedawcy B: 17, 23, 13, 24, 33, 21, 18, 16, 32. Zweryfikować H0 na poziomie istotności α0,05.
Przykład 3 (wartości cechy wyrażone są w skali porządkowej):
Dwie reklamy należy porównać ze względu na ich siłę oddziaływania. Wybrano losowo próbę 8 osób i zanotowano ich reakcję na reklamę nr 1 (punktacja w skali 1 do 10): 7, 8, 6, 7, 9, 5, 10. Następnie wylosowano inne 9 osób i zanotowano ich reakcję na reklamę nr 2: 3, 4, 8, 5, 7, 2, 5, 6. Zweryfikować H0 o jednakowym oddziaływaniu reklam, wobec H1, że jedna reklama oddziałuje bardziej od drugiej.
Przykład 4 (wartości cechy wyrażone są w skali porządkowej):
Do finału konkursu szybkiego czytania dotarło 9 osób, z których 5 szkoliło się wykorzystując metodę A, a 4 metodę B. Skuteczność metody szkolenia ocenia się za pomocą liczby błędów popełnionych w odpowiedzi na pytania kontrolne związane z treścią tekstu konkursowego. Im mniej błędów, tym skuteczność danej metody jest większa. Na podstawie wyników sprawdzić zasadność przypuszczenia, że metoda A jest mniej efektywna niż metoda B. Punkty dla metody A: 3, 7, 9, 4, 6 oraz dla metody B: 6, 3, 4, 2.
Przykład 5 (zmienna losowa wyrażona w skali ilorazowej lecz rozkład jest asymetryczny):
Porównanie jakości dwóch wkrętarek elektrycznych sterowanych elektronicznie. Porównaniu poddaje się wartości dynamicznego momentu dokręcania.
Sposób postępowania (obliczenia w programie MS Excel)
Przykład 6 (wartości cechy wyrażone są w skali porządkowej):
Do firmy z sektora motoryzacyjnego w celu uzupełnienia personelu działu produkcji, przyjęto 21 nowych pracowników. W pierwszym dniu pracy odbyło się szereg szkoleń. Pracowników podzielono pomiędzy 2 Trenerów, którzy prowadzili szkolenia w osobnych salkach. Po szkoleniach przeprowadzono test wiedzy pracowników. Punktacja testu w skali od 0 do 20 punktów. Wyniki testu dla Trenerów przedstawiono w poniższej tabeli. Na poziomie istotności α0,05 sprawdzić, czy efektywność szkolenia obydwóch Trenerów jest taka sama.

Na Rys.1 przedstawiono wyniki testów nowych pracowników z podziałem na odpowiedniego Trenera. Policzono liczności obydwóch próbek (komórki A16 i B16), zgodnie ze wzorem (1) wartość oczekiwaną (komórka B18) oraz zgodnie ze wzorem (2) wariancję (komórka B19). Formuły obliczeniowe przedstawiono w kolumnie C.
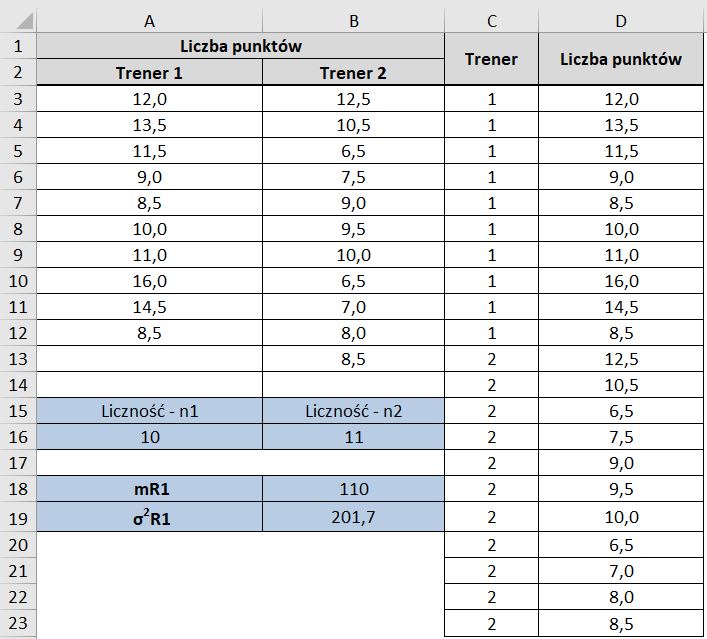
Do kolumny C (Rys. 2) wprowadzono cyfry 1 i 2 oznaczające danego Trenera, natomiast do kolumny D pomiary kopiowane z kolumn A i B tworząc łączny zbiór wartości (punktów).
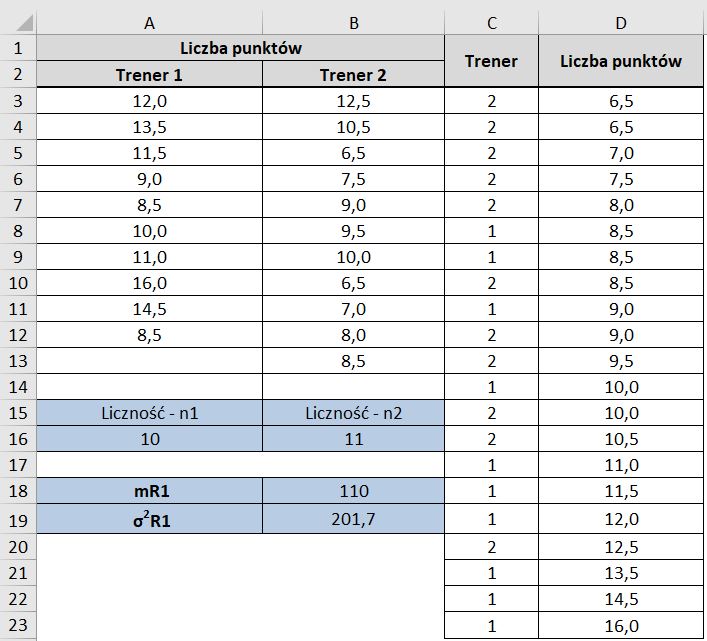
Na Rys.3 kolumny C i D posortowano rosnąco wg kolumny D.
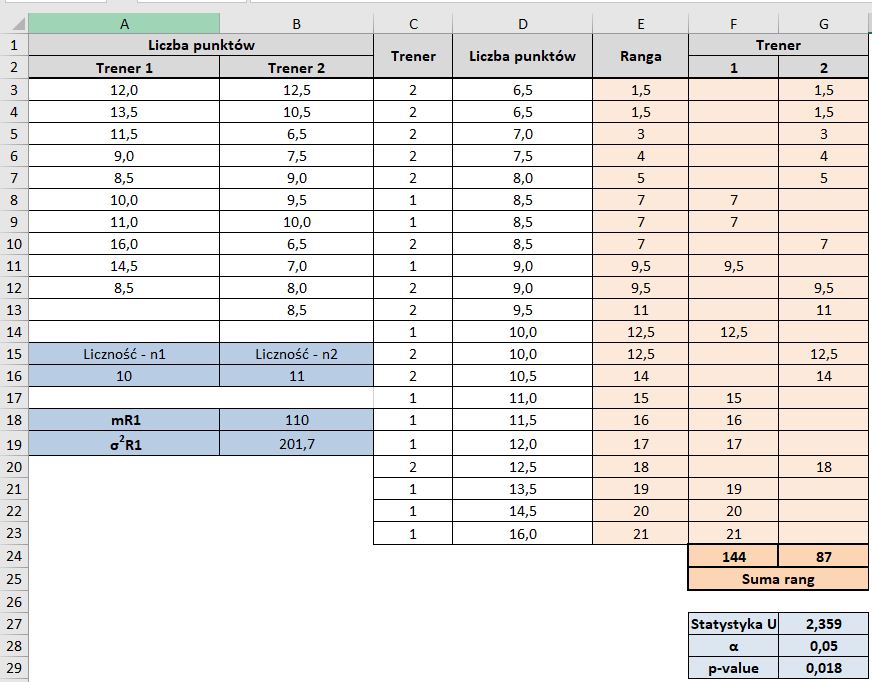
W kolumnie E przeprowadzono operację rangowania. Do tego celu wykorzystano następującą formułę:
=(PODAJ.POZYCJĘ(D3;$D$3:$D$23;0)+PODAJ.POZYCJĘ(D3;$D$3:$D$23;1))/2
Formułę wprowadzono do komórki E3 a następnie kopiowano aż do komórki E23.
Po prawidłowo wykonanym rangowaniu dokonano rozdzielenia rang na grupy odpowiadające obydwom próbom. W związku z tym do komórki F3 wprowadzono formułę: =JEŻELI(C3=$F$2;E3;””), do komórki G3 formułę: =JEŻELI(C3=$G$2;E3;””) Powyższe formuły kopiowano aż do komórek F23 i G23.
W komórkach F24 oraz G24 policzono sumy rang. W komórce G27 policzono wartość statystyki U wg wzoru (3): =(F24-B18-0,5)/PIERWIASTEK(B19) Ponieważ suma rang próby 1 (144) jest wyższa od mR1 (110) wartość 0,5 znajdującą się w liczniku wzoru odjęto.
Do komórki G28 wprowadzono wartość poziomu istotności statystycznej a następnie wykorzystując formułę =(1-ROZKŁAD.NORMALNY.S(G27))*2 w komórce G29 policzono wartość p-value. Taka postać formuły jest konsekwencją wnioskowania z dwustronnym obszarem krytycznym.
Wniosek
Ponieważ p-value(0,018) < α0,05 hipotezę zerową o jednakowych umiejętnościach szkoleniowych obydwóch Trenerów należy odrzucić. Punktacja grupy pracowników szkolonych przez Trenera nr 1 jest istotnie wyższa niż pracowników szkolonych przez Trenera nr 2.
Sposób postępowania (obliczenia w programie Minitab)
W programie Minitab należy wybrać ścieżkę: Stat – Nonparametrics – Mann-Whitney.
Do odpowiednich okien należy wprowadzić pierwszą i drugą próbkę, wybrać zakres przedziału ufności oraz dokonać wyboru odpowiedniej hipotezy alternatywnej (H1). Wybierając przycisk OK otrzymuje się wynik analizy taki, jaki przedstawiono na Rys. 5:
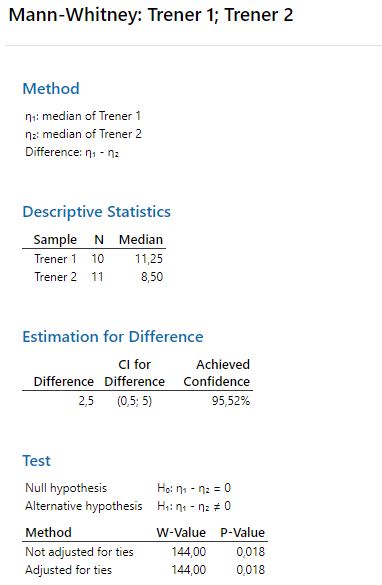
W tym miejscu należy zaznaczyć, że program Minitab testuje różnice median. Nie jest to do końca prawdą, ponieważ można łatwo wykazać, że testując dwie próby, których mediany będą miały takie same wartości w wyniku testu, próby te będą istotnie różne (p-value<alfa0,05).
W celu wizualizacji danych przygotować można wykres (Rys. 6) wartości indywidualnej dla rozkładów obydwóch prób. Dodatkowo na wykres nanieść można wartości median, aby wskazać różnicę pomiędzy wartościami przeciętnymi każdej próby.
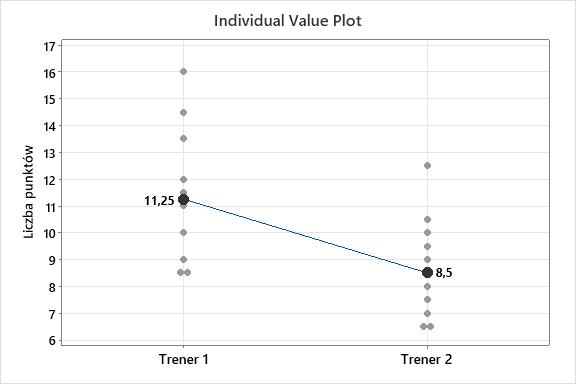
Podsumowanie
W artykule przedstawiono nieparametryczny test Manna-Whitneya dla dwóch prób o niewielkiej liczności. W takiej sytuacji, z praktycznego punktu widzenia wystarczające jest zastosowanie rangowania zwykłego, tak jak to przedstawiono w obliczeniach z wykorzystaniem programu MS Excel.
Jeżeli jednak liczności obydwóch prób będą większe, należy wtedy oprócz rangowania zwykłego, dokonać także operacji rangowania wiązanego i do obliczenia wariancji zastosować wzór (4), co wymaga z kolei ustalenia zarówno liczby grup rang wiązanych g, jak i wchodzących w ich skład współczynników tj.
Jeżeli chcesz otrzymać gotowy kalkulator testu Manna-Whitneya przygotowany w programie MS Excel , zawierający rangi wiązane, to napisz na nasz adres: biuro@pstconsulting.pl
Plik wyślemy Ci pocztą elektroniczną.
Materiały wykorzystane w artykule zaczerpnięte zostały z książki: Weryfikacja hipotez statystycznych wspomaganych komputerowo, Marian Maliński, Gliwice 2004.
.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to udostępnij go w mediach społecznościowych:
Zaufali nam:
.
Co mówią nasi zadowoleni Klienci:
.
W przypadku pytań zapraszamy do kontaktu:
.
