Metoda Taguchi z optymalizacją operacji dokręcania

Metoda Taguchi to sposób przeprowadzania analizy optymalizacyjnej z wykorzystaniem ortogonalnego planu eksperymentu.
Metoda Taguchi – wstęp
Celem artykułu jest pokazanie w jaki sposób dobrać takie nastawy wkrętarek elektrycznych, aby gwarantowały wysoką jakość dokręcania przy jednoczesnym skróceniu czasu cyklu operacji.
Łączenie elementów odbywa się za pomocą dokręcania, w którego finale osiąga się wymaganą siłę osiową (siłę docisku, ang. clamping force) powodującą wzajemne, odpowiednio silne ich doleganie. Sztuką jest zapewnienie powtarzalności tej siły, ponieważ realizuje się to poprzez dokręcenie na precyzyjnie wyznaczony moment lub kąt obrotu. Niestety pomimo precyzyjnego dokręcania wartość siły osiowej nie jest powtarzalna i podlega pewnemu rozproszeniu (wariancji). Rozproszenie to można minimalizować poprzez optymalizację, polegającą na doborze odpowiednich parametrów programu elektrycznego narzędzia dokręcającego.
W niniejszym artykule przedstawiony został sposób przeprowadzania analizy optymalizacyjnej z wykorzystaniem ortogonalnego planu eksperymentu – metoda Taguchi. Wykonany eksperyment miał na celu sprawdzenie zależności pomiędzy nastawami wybranych parametrów dokręcania a obliczoną na podstawie pomiarów kąta dokręcania wartością wskaźnika S/N (ang. Signal to Noise ratio). Wartość tego wskaźnika informuje o rozproszeniu danych. Poszukuje się takich nastaw elektrycznej wkrętarki dokręcającej, aby wartość S/N była jak najwyższa – optymalizacja parametrów dokręcania ma na celu maksymalizację tego wskaźnika.
Metoda Taguchi – charakterystyka procesu dokręcania
Celem dokręcania jest uzyskanie optymalnej i powtarzalnej siły osiowej wywołującej określony docisk łączonych elementów poprzez wzgląd na istnienie wielu czynników (niektóre przedstawiono na Rys. 1.) mających bezpośredni wpływ na współczynnik tarcia, a przez to na wartość uzyskanej siły osiowej, optymalizacja procesu dokręcania jest czynnością wymagającą znajomości podstaw statystyki.
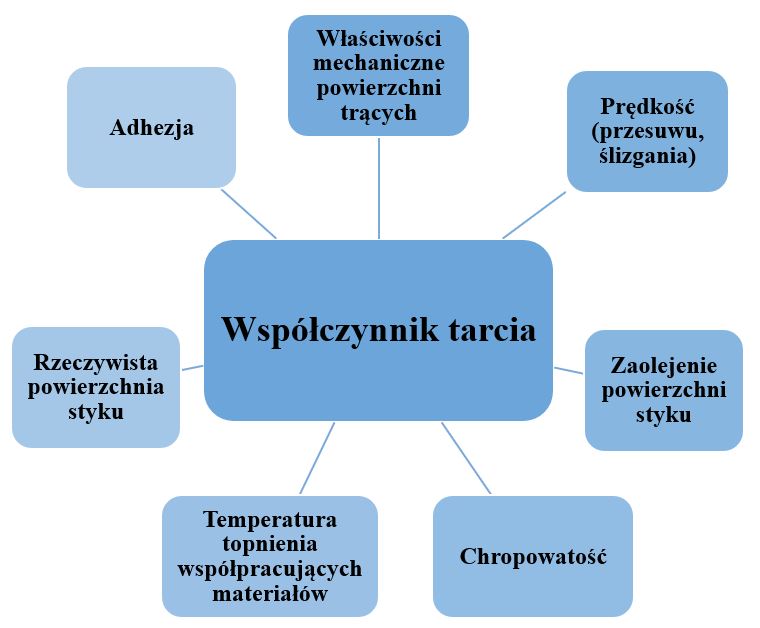
Nowoczesne przedsiębiorstwo, realizujące proces dokręcania w formie masowej (nawet kilkaset tych samych dokręceń na dobę) zaopatrzone jest w nowoczesne narzędzia dokręcające mające możliwość programowania odpowiednich, optymalnych nastaw wkrętarki.
Operację dokręcania przykładowej śruby (schemat przedstawiono na Rys. 2.) można podzielić na dwie fazy:
- Faza wstępna, w której śruba dokręcana jest swobodnie do czasu dotknięcia łba śruby do powierzchni elementu łączonego (tzw. faza rundown).
- Faza końcowa, w której śruba dokręcana jest od końca fazy pierwszej do osiągnięcia finalnego momentu dokręcenia.
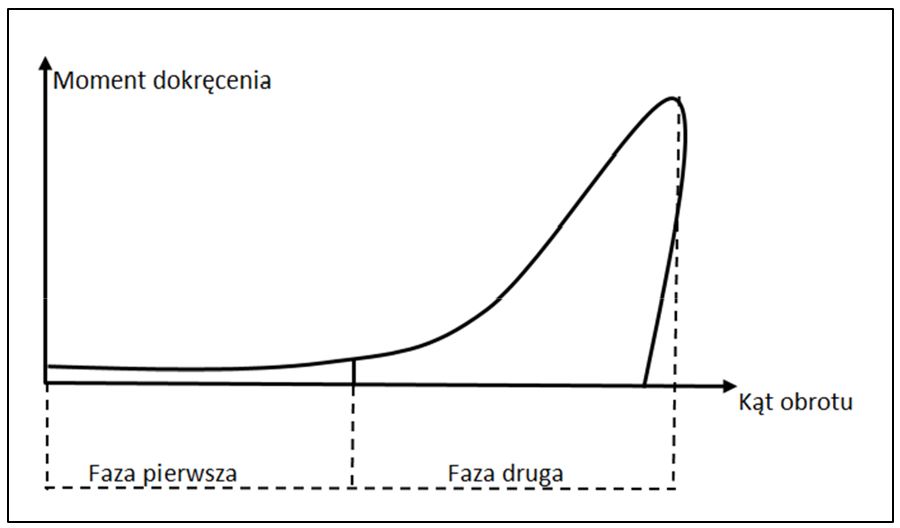
Dokręcając na określony moment Nm nadzorować i minimalizować należy zmienność finalnego kąta (kąt obrotu, w którym osiągany jest moment dokręcania), którego wartość jest zmienną losową podlegającą określonej fluktuacji. Z punktu widzenia jakości dokręcania, rozkład kąta dokręcania powinien znajdować się pomiędzy dwoma granicami obliczonymi na podstawie odpowiednio licznej próby losowej.
Metoda Taguchi – charakterystyka parametrów programu narzędzia dokręcającego (wkrętarki elektrycznej)
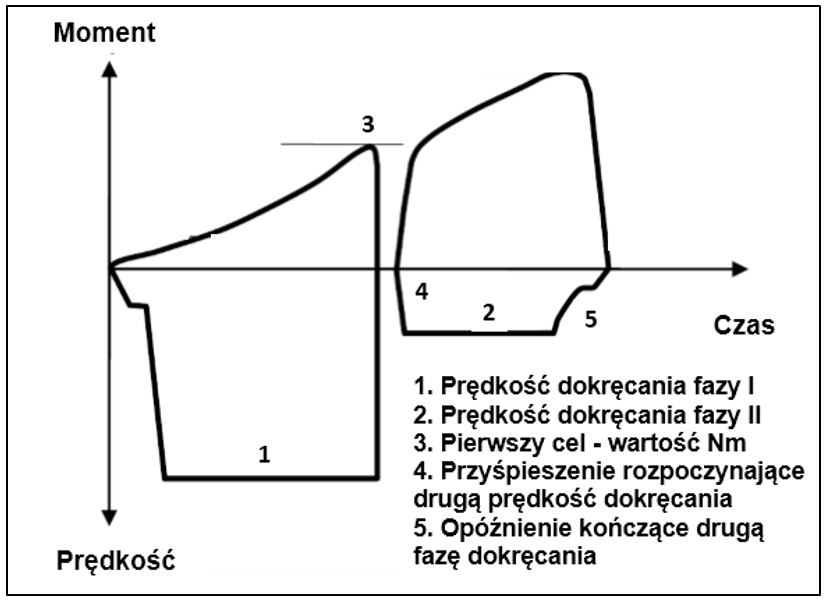
Parametry programu narzędzia (Rys.3.), mające wpływ na zmienność rozkładu kąta opisać można następująco:
- Prędkość dokręcania w pierwszej fazie – (nazywana także pierwszym krokiem dokręcania) – obrotowa prędkość narzędzia, której wartość rpm (z ang. revolutions per minute) w dużej mierze zależy od czasu cyklu operacji na stanowisku montażowym.
- Prędkość dokręcania w drugiej fazie – obrotowa prędkość narzędzia, której wartość rpm w dużej mierze zależy od rodzaju (materiału) łączonych elementów, a także od twardości złącza. W drugiej fazie prędkość powinna być mniejsza niż w pierwszej.
- Pierwszy cel – wartość momentu (Nm) zmiany prędkości pierwszej na drugą – w ściśle określonej wartości momentu następuje redukcja prędkości obrotowej, której celem jest zwiększenie precyzji dokręcania, a także redukcji zjawiska relaksacji.
- Przyśpieszenie rozpoczynające drugą prędkość dokręcania – cecha ta może mieć istotne znaczenie w przypadku połączeń sztywnych, w których przyrost wartości momentu w stosunku do wartości kąta jest wysoki (do 30 stopni).
- Opóźnienie kończące drugą fazę dokręcania – parametr ten, w zależności od rodzaju połączenia może mieć negatywny lub pozytywny wpływ na zmienność kąta finalnego, ponieważ jego użycie ma na celu zmniejszenie prędkości obrotowej narzędzia bezpośrednio przed osiągnięciem momentu dokręcania.
W celu minimalizacji rozproszenia kąta finalnego wyżej wymienione parametry powinny być ustawiane indywidualnie dla każdego połączenia gwintowego. Na Rys.3. przedstawiono graficzne wytłumaczenie parametrów.
Design of Experiment – Planowanie Eksperymentu
Planowanie doświadczeń na ogół jest taką strategią planowania eksperymentu, iż poprawne i trafne wnioskowanie można osiągnąć w sposób efektywny i ekonomiczny, ponieważ wybór właściwego planu doświadczenia powinien zależeć od dostępnych zasobów materialnych, czasowych czy personalnych. Prawidłowo zaprojektowane i wykonane doświadczenie będzie często prowadzić do względnie prostej analizy statystycznej oraz interpretacji wyników.
Doświadczenia czynnikowe (dwu i więcej) dostarczają badaczowi metodologie badania współzależności między wieloma badanymi czynnikami. Oprócz określenia zmienności czynnika często wynikiem eksperymentu jest potwierdzenie istotności statystycznej interakcji pomiędzy czynnikami.
Planując doświadczenie należy ograniczyć obciążenia, jakie wprowadzają warunki doświadczenia. Takie zagadnienia, jak randomizacja i bloki są związane z minimalizacją efektów zakłócających lub czynników ubocznych.
Dobry plan doświadczenia powinien:
- uwzględnić posiadaną wiedzę i doświadczanie w doborze czynników, ich poziomów i formułowaniu założeń,
- dostarczyć trafnych informacji przy minimum wysiłku,
- zapewnić przed rozpoczęciem doświadczenia, iż układ jest w stanie osiągnąć cel doświadczenia z wymaganą dokładnością,
- odzwierciedlać sekwencyjny charakter większości badań,
- określić zarówno ułożenie, jak i kolejność nastaw doświadczalnych celem uniknięcia nieporozumień podczas trwania doświadczenia.
Cel i zakres badań
Analiza wpływu zmiany nastaw parametrów procesu dokręcania na wartość wskaźnika S/N obliczonego jako:
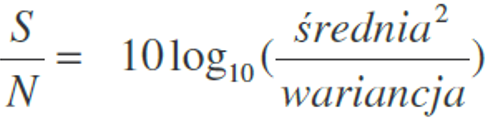
Połączeniem gwintowym poddanym optymalizacji w tym przypadku był montaż elementu zawieszenia samochodu do nadwozia. Dokręcanie realizowane w strategii momentowej (dokręcanie na określoną wartość momentu), gdzie fluktuacji podlegała wartość kąta finalnego. Celem eksperymentu było wyznaczenie takich nastaw dla czynników głównych, aby wartość wskaźnika S/N była jak najwyższa. Eksperyment, prowadzony zgodnie z zasadami DoE (planowania eksperymentu), polegał na zbadaniu wpływu czterech czynników:
- X1: Prędkość 1 – to prędkość pierwszego kroku dokręcania [rpm].
- X2: Prędkość 2 – to prędkość drugiego (finalnego) kroku dokręcania [rpm].
- X3: Pierwszy cel – to wartość momentu dokręcania [Nm], w którym następuje zmiana prędkości obrotowej narzędzia (zmiana fazy dokręcania z pierwszej na drugą).
- X4: Krok opóźnienia – wartość prędkości obrotowej narzędzia, uzyskiwana bezpośrednio przed osiągnięciem finalnego momentu dokręcania. To zmiana prędkości w końcowej fazie drugiego kroku dokręcania, głównie w celu poprawy precyzji dokręcania.
Eksperyment przeprowadzono wg algorytmu: 24*2, gdzie:
- 2X*X – ilość poziomu nastaw każdego czynnika.
- X4*X – ilość czynników w eksperymencie.
- XX*2 – ilość powtórzeń dla poszczególnej konfiguracji (nastaw) czynników.
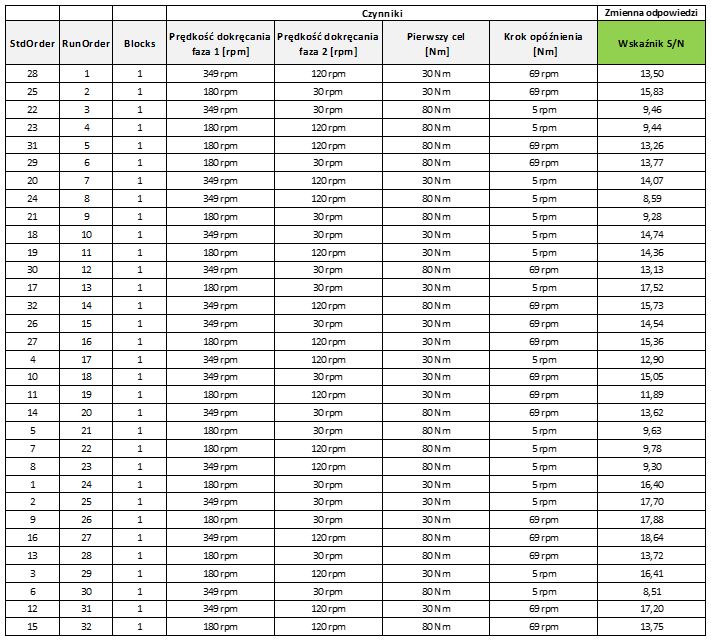
Na Rys.4. przedstawiono plan eksperymentu, w którym przedstawiono losowo dobrane zestawy nastaw czynników. Kolumna ostatnia to wynik eksperymentu, czyli wartości wskaźnika S/N dla każdej nastawy, uzyskane na podstawie 30 elementowej próby losowej tj. pojedynczych wartości finalnego kąta dokręcania. Pomiary zebrane zostały na stanowisku montażowym, odczytane bezpośrednio ze sterownika narzędzia dokręcającego.
Analiza wyników
Wykres Pareto (Rys.5.) – przedstawia uszeregowane w ciągu malejącym pod względem wartości statystyki testu t-Studenta, czynniki oraz interakcje. Czerwona linia to wartość krytyczna testu obliczona na poziomie istotności α0,05. Czynniki oraz interakcje, których kolumny przekraczają tę linię, są istotne statystycznie.
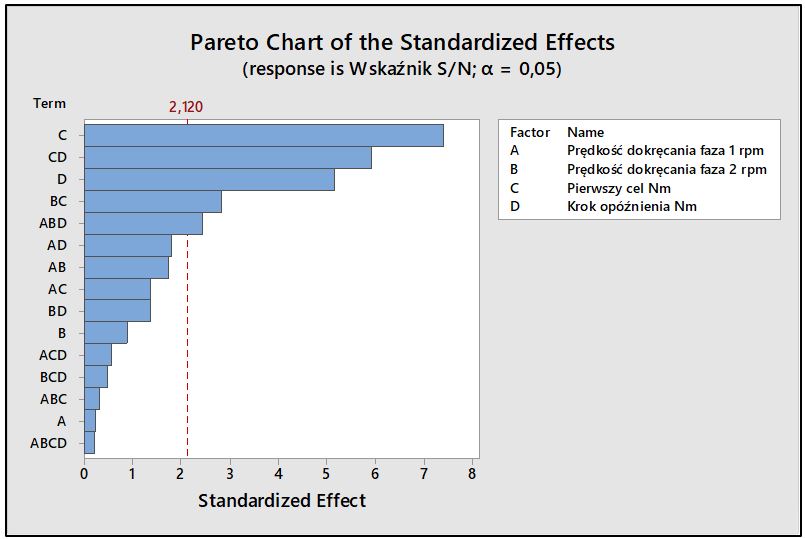
Z Rys.5. wnioskować należy, iż zmienne, które wywierają istotny statystycznie wpływ na wskaźnik S/N to:
- Czynnik C – pierwszy cel, wartość momentu, w którym następuje zmiana prędkości obrotowej narzędzia dokręcającego.
- Interakcja drugiego rzędu pomiędzy czynnikiem C (pierwszy cel) a czynnikiem D (krok opóźnienia).
- Czynnik D – krok opóźnienia.
- Interakcja drugiego rzędu pomiędzy czynnikiem B (prędkość dokręcania w fazie 2) a czynnikiem C (pierwszy cel).
- Interakcja trzeciego rzędu pomiędzy czynnikiem A (prędkość dokręcania w fazie 1) a czynnikiem B (prędkość dokręcania w fazie 2) oraz czynnikiem D (krok opóźnienia).
Rys. 6. zawiera wykresy, na których przedstawiono średni wpływ czynników głównych. Zauważyć należy brak różnicy pomiędzy wartościami średnimi poziomów dla czynników A (prędkość pierwszego kroku dokręcania) oraz B (prędkość drugiego kroku dokręcania). Natomiast w przypadku:
- Czynnika C (pierwszy cel) – zauważyć należy istotną różnicę: ustawiając moment przejścia z fazy 1 do 2 dokręcenia na wartość 30 Nm, oczekiwać można wartości wskaźnika S/N na wyższym poziomie wynoszącym przeciętnie 15,33.
- Czynnika D (krok opóźnienia) – przy zwiększeniu wartości prędkości obrotowej do wynoszącej 69 rpm, oczekiwać można wzrostu wartości wskaźnika S/N do przeciętnego poziomu 14,80.

Na Rys. 7. przedstawiono wykres interakcji podwójnej pomiędzy czynnikiem C (pierwszy cel dla momentu) a czynnikiem D (krok opóźnienia). Zauważyć należy, iż do silnej i niekorzystnej interakcji powodującej obniżenie wskaźnika S/N do przeciętnie 9,24 dochodzi w sytuacji, w której:
- Nastawa czynnika C wynosi 80 Nm.
- Nastawa czynnika D wynosi 5 rpm.
Dodać należy, iż to czynnik D (krok opóźnienia) jest czynnikiem bardziej „wrażliwym” na zmianę nastaw.

Rys. 8. przedstawia wykres interakcji podwójnej pomiędzy czynnikiem B a czynnikiem C. Zauważyć należy, iż do korzystnej interakcji powodującej wzrost wartości wskaźnika S/N do przeciętnie 16,20 dochodzi w sytuacji, w której:
- Nastawa czynnika C wynosi 30 Nm.
- Nastawa czynnika B wynosi 30 rpm.

Metoda Taguchi – regulacja nastaw parametrów dokręcania
W wyniku przeprowadzonego eksperymentu, a także uwzględniając czas cyklu operacji, zaproponowano korektę nastaw dla parametrów dokręcania:
- Pierwszy czynnik A (prędkość dokręcania w fazie 1) ustawiono na wartość 300 rpm. Ponieważ czynnik ten nie wywierał istotnego wpływu na wartość wskaźnika S/N, prędkość dokręcania można było dostosować ze względu na czas cyklu operacji na stanowisku montażowym.
- Drugi czynnik B (prędkość dokręcania w fazie 2) ustawiono na wartość 30 rpm.
- Trzeci czynnik C (pierwszy cel dla momentu przejścia z fazy 1 do 2) ustawiono na wartość 30 Nm.
- Czwarty czynnik D (krok opóźnienia) ustawiono na wartość 69 rpm.
Uwzględniając nowe nastawy parametrów dokręcania wkrętarki elektrycznej, wykonano próbę o liczności 200 dokręceń, a dane z próby porównano z danymi pochodzącymi z dokręceń przed wykonaniem eksperymentu. Na Rys. 9. porównano rozkłady danych finalnego kąta dokręcania.

Dodatkowo policzono i porównano następujące statystyki:
| Statystyki | Przed eksperymentem | Po eksperymencie |
| Statystyka testu normalności Andersona-Darlinga | 15,68 | 1,33 |
| Estymator skośności | 2,27 | 0,62 |
| Klasyczny współczynnik zmienności | 9,0% | 4,1% |
Wszystkie trzy statystyki są korzystniejsze dla próby po eksperymencie:
Niższa wartość statystyki testu normalności Andersona-Darlinga wskazuje, iż rozkład danych jest bardziej zbliżony do rozkładu normalnego.
Niższa wartość estymatora skośności (bliżej zera) wskazuje na bardziej symetryczny kształt histogramu.
Ponad dwukrotnie niższa wartość klasycznego współczynnika zmienności informuje o ponad dwukrotnie niższym rozproszeniu danych.
W wyniku optymalizacji parametrów dokręcania, na podstawie 200 elementowej próby policzono i zaproponowano wstępne granice dla kąta finalnego.
Rozkład danych wraz z granicami przedstawiono na Rys. 10. Granice podlegają rekalkulacji po osiągnięciu liczniejszej próby, np. 500 i 1000 elementowej.

Metoda Taguchi – wnioski
- Zmienność finalnego kąta dokręcania podlega możliwości poprawy poprzez optymalny dobór nastaw tych parametrów programu dokręcania, które wywierają wpływ na jego fluktuację.
- Zaplanowanie i przeprowadzenie optymalizacji zgodnie z zasadami DoE umożliwia szybką i precyzyjną identyfikację czynników powodujących zmienność finalnego kąta dokręcania.
- Wykonując eksperyment zgodnie z zasadami DoE, zyskuje się statystyczne prawdopodobieństwo, iż rozkład kąta finalnego jest optymalny. Dla takiego rozkładu o wiele bardziej precyzyjnie można obliczyć granice, których celem jest prewencja przed powstaniem błędów dokręcania. Narzędzie elektryczne przestaje być tylko wkrętarką, ale staje się zaawansowanym systemem error proofing mającym za zadanie eliminację błędów montażowych jeszcze na stanowisku pracy.
- Precyzyjnie obliczone granice kontrolne służą do eliminacji wad takich jak: zbyt niska (poza specyfikacją) twardość śruby czy nakrętki, wady gwintu, wady powłoki stabilizującej współczynnik tarcia na śrubie, wady geometryczne otworu gwintowego w dokręcanym elemencie, itp.
- Podobny eksperyment prowadzony powinien być również dla fazy wstępnej dokręcania (tzw. fazy rundown), gdzie poprzez precyzyjnie obliczone granice można wykryć wady takie jak: zbyt krótka lub zbyt długa śruba, brak podkładki, nadmiar podkładki, użycie nieodpowiedniej nakrętki (np. bez elementu plastikowego tzw. threadlocka), śruba lub nakrętka z nieodpowiednim skokiem gwintu, itp.
- W niniejszym artykule opisano liniowy sposób analizy wpływu czynników na wartość wskaźnika S/N.
Autor: dr inż. Rafał Popiel
Jeżeli artykuł Ci się podobał, to podziel się nim proszę w mediach społecznościowych:
Więcej informacji zdobyć można na naszym szkoleniu:
Zaawansowane techniki dokręcania łączników gwintowych
Zaufali nam
.
